Dynamics Generalisation with Behaviour Foundation Models

Training Agents with Foundation Models Workshop

Scott Jeen & Jonathan M. Cullen

University of Cambridge, UK

2024-08-09

Introduction

• Building RL agents that generalise to unseen dynamics is hard!

• Behaviour foundation models (BFMs) can return optimal policies for any unseen reward function in principle [1]

• Certain changes in dynamics functions can be codified as changes in reward functions [2]

• Can we use a BFM to return policies for reward functions that represent changed dynamics? If so, we’d generalize to unseen dynamics functions!

[1] Ahmed Touati, Jérémy Rapin, and Yann Ollivier. Does zero-shot reinforcement learning exist? ICLR 2023

[2] Benjamin Eysenbach, Swapnil Asawa, Shreyas Chaudhari, Sergey Levine, and Ruslan Salakhutdinov. Off-dynamics reinforcement learning: Training for transfer with domain classifiers. ICLR 2021

Problem Setup

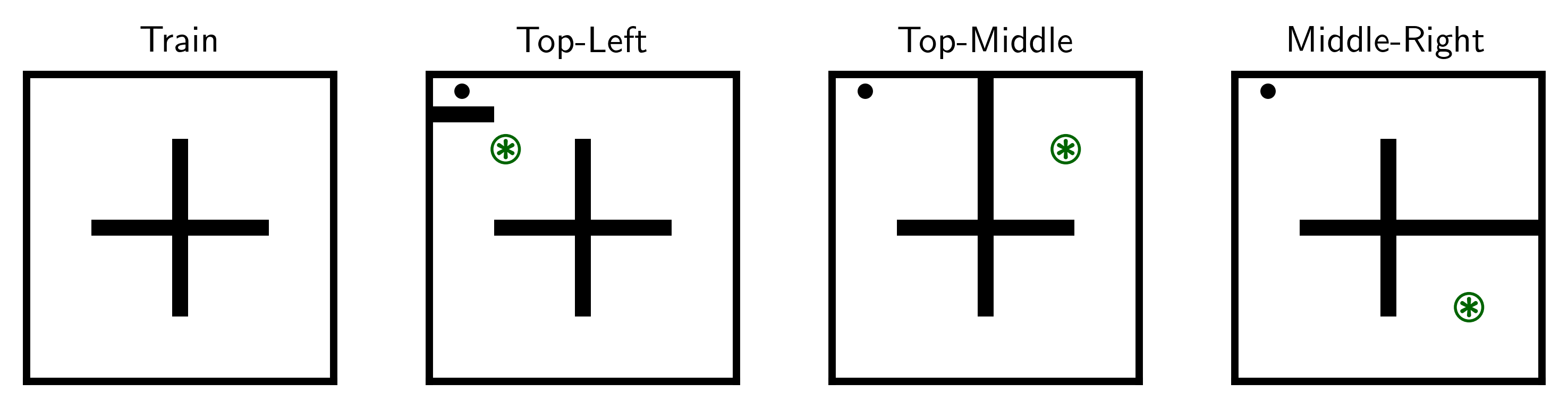
1. Pre-train \(\pi(s,z)\) on offline dataset \(D_{\text{train}}\) from one env
2. Collect datasets of transitions from \(N\) test envs \(\{D_{\text{test}}^1, \ldots, D_{\text{test}}^N\}\)
3. Use \(\{D_{\text{test}}^1, \ldots, D_{\text{test}}^N\}\) to condition \(\pi(s, z)\) on test envs with changed dynamics

[3] Denis Yarats, David Brandfonbrener, Hao Liu, Michael Laskin, Pieter Abbeel, Alessandro Lazaric, and Lerrel Pinto. Don’t change the algorithm, change the data: Exploratory data for offline reinforcement learning. arXiv preprint arXiv:2201.13425, 2022.

Method: Contextual BFMs

• Idea
• Protocol

BFMs conventionally infer \(z\) from \(D_{\text{train}}\) via:

\(z \approx \mathbb{E}_{(s_t, a_t, s_{t+1}) \sim D_{\text{train}}} \big[R(s_t, a_t, s_{t+1}) B(s_t, a_t, s_{t+1})\big]\)

Key idea: downweight \(R\) for transitions not possible under changed dynamics

(a) \(\pi(s,z)\) is pre-trained (b) \(D_{\text{test}}\) is collected in each test env and transitions not possible in the train env are downweighted (c) \(z\) is inferred from \(D_{\text{test}}\) and passed to \(\pi(s,z)\).

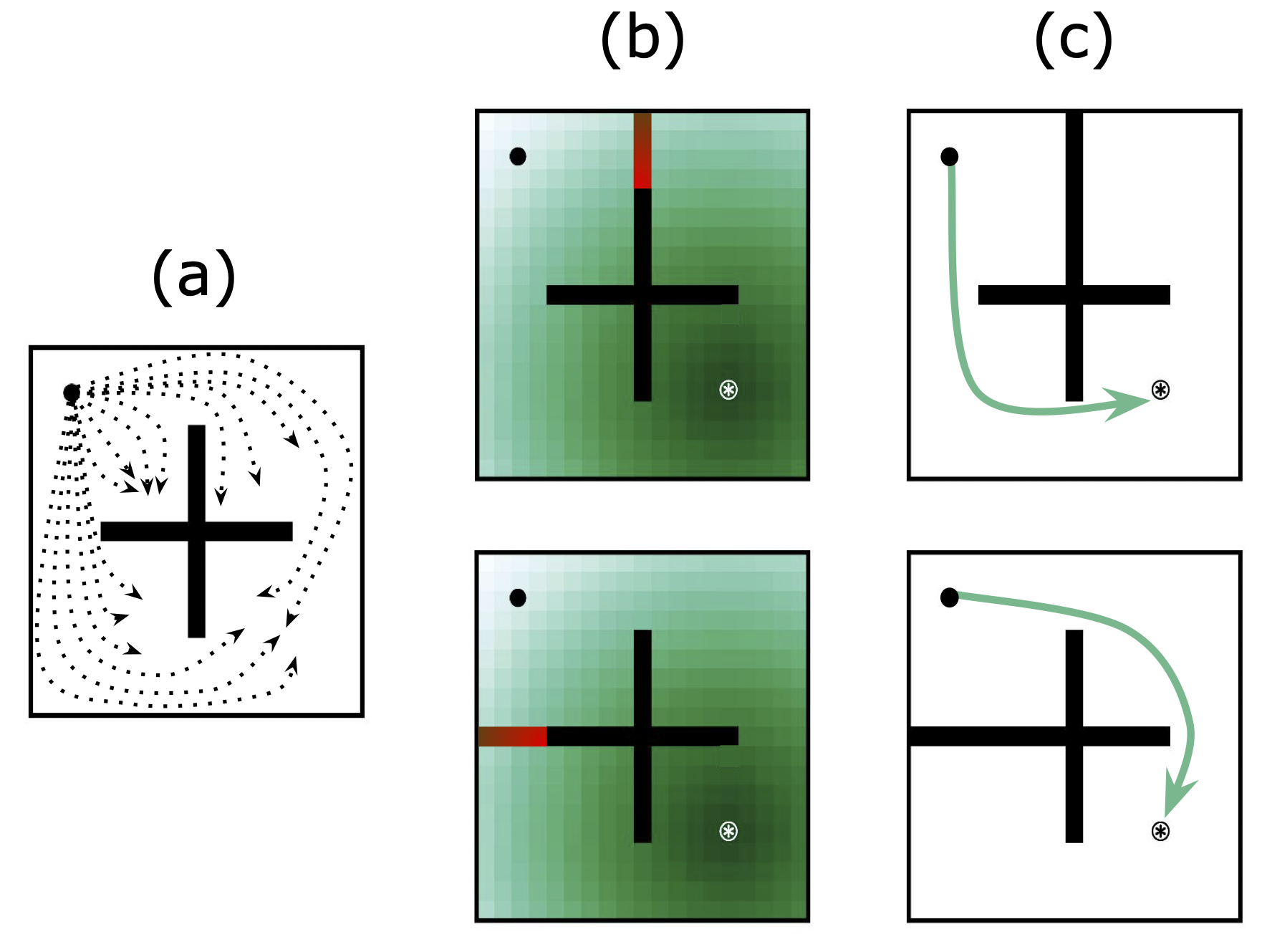
1. Collect \(\{D_{\text{test}}^1, \ldots, D_{\text{test}}^N\}\).

2. Train classifiers \({\color{blue}{f_{(s_t,a_t)}}}\) and \({\color{red}{f_{(s_t,a_t,s_{t+1})}}}\) to distinguish between train and test envs.

3. Calculate reward augmentation for each transition (from [2]): \({\color{green}{\Delta R}} = {\color{red}{\log p (test|s_t, a_t, s_{t+1})}} - {\color{blue}{\log p(test|s_t, a_t)}}\) \(- {\color{red}{\log(train | s_t, a_t, s_{t+1})}} + {\color{blue}{\log p(train | s_t, a_t)}}\)

4. Infer z with augmented rewards:

\(z \approx \mathbb{E}_{(s_t, a_t, s_{t+1}) \sim D_{\text{train}}} \big[(R(s_t, a_t, s_{t+1}) + {\color{green}{\Delta R}}) B(s_t, a_t, s_{t+1})\big]\)

5. Pass \(z\) to \(\pi(s,z)\)

Preliminary Results

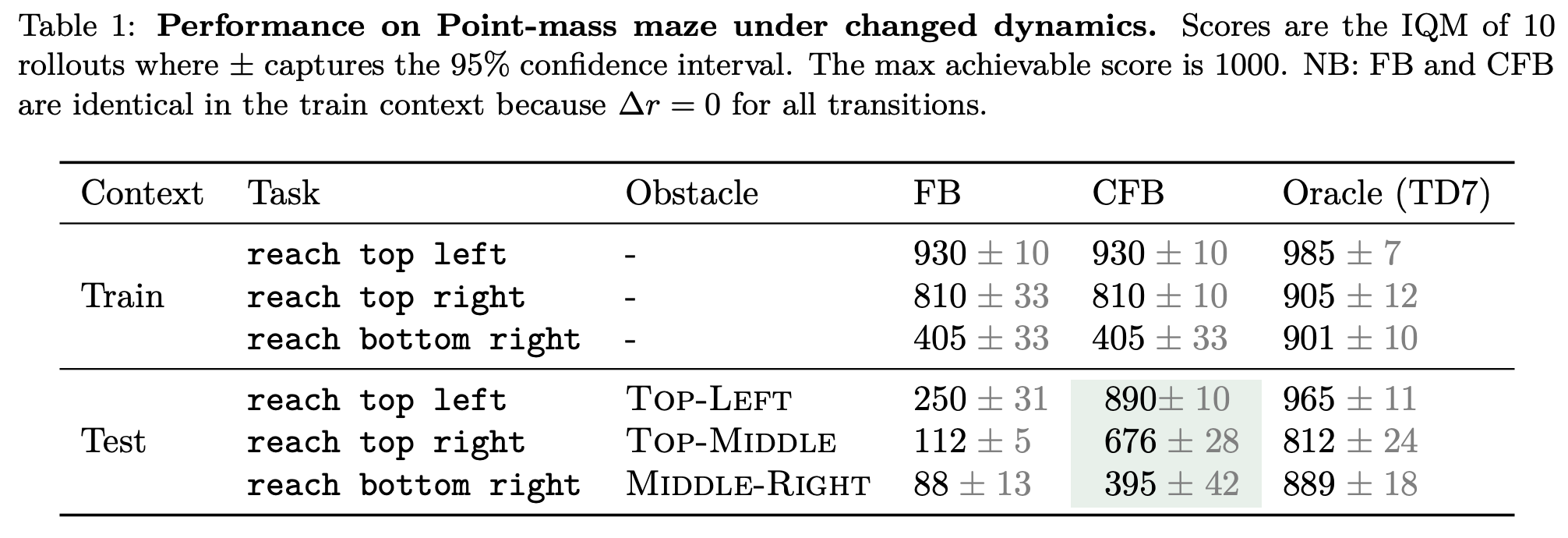
Limitations

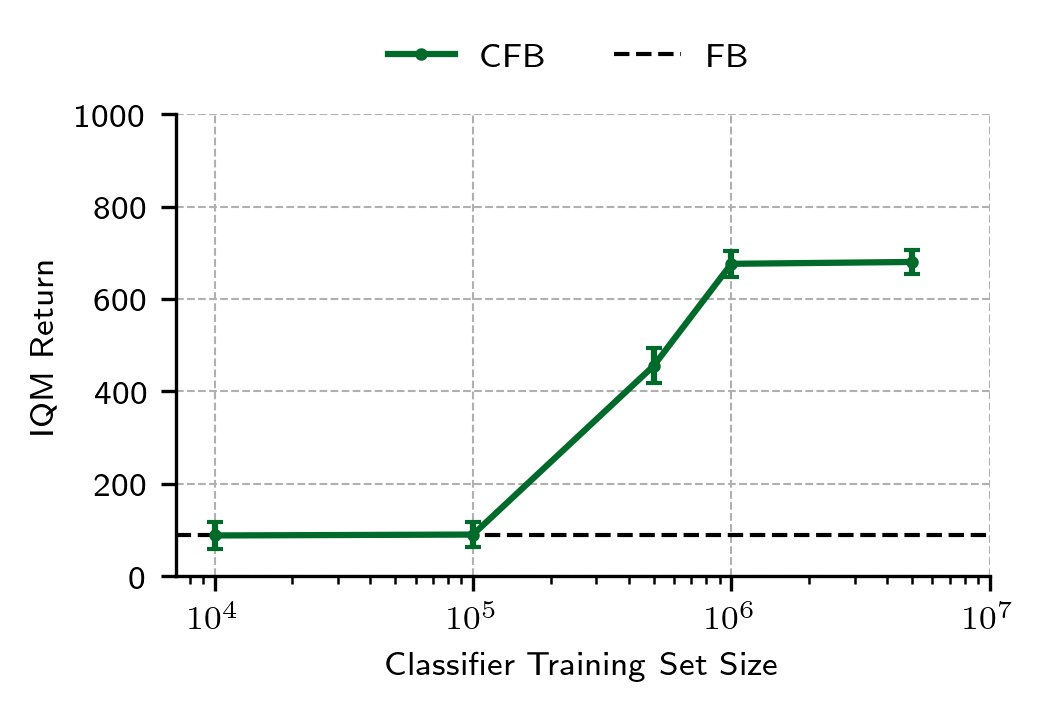
Conclusions

✅ Contextual BFMs can return performant policies for dynamics not seen during training

❌ The classifier training sets need to be large (\(>10^6\) transitions) to achieve this (in our experiments)

Thanks!

Paper

Twitter: @enjeeneer

Website: https://enjeeneer.io