On Zero-Shot Reinforcement Learning

PhD Viva

Scott Jeen

University of Cambridge

Outline

1. The Case for Zero-Shot RL

2. Chapter 3: From Low Quality Data

3. Chapter 4: Under Changed Dynamics

Outline

1. The Case for Zero-Shot RL

2. Chapter 3: From Low Quality Data

3. Chapter 4: Under Changed Dynamics

3. Chapter 4: Under Partial Observability

4. Chapter 5: With No Prior Data

5. Outlook

The Case for RL

• Society faces problems, many of which can be cast as sequential decision-making problems:

- Engineering: energy generation control (fusion, fission, wind)

- Education: teacher-student interaction

- Mathematics: theorem-proving

- Policy: climate negotiations

- Science: forming hypotheses -> making predictions -> testing them

• In such cases:

- System dynamics are rarely known (so standard control theoretic approaches can't be applied)

- Data demonstrating the optimal policy is rarely available (so we can't imitate the optimal policy with supervised learning)

- It is much easier to evaluate a solution that generate one (i.e. there exists a generator-verifier gap)

• RL provides a generic framework for modelling sequential-decision making problems with these characteristics [1]

RL + Perfect Simulators + Compute = Superhuman

David Silver, RL Conference 2024

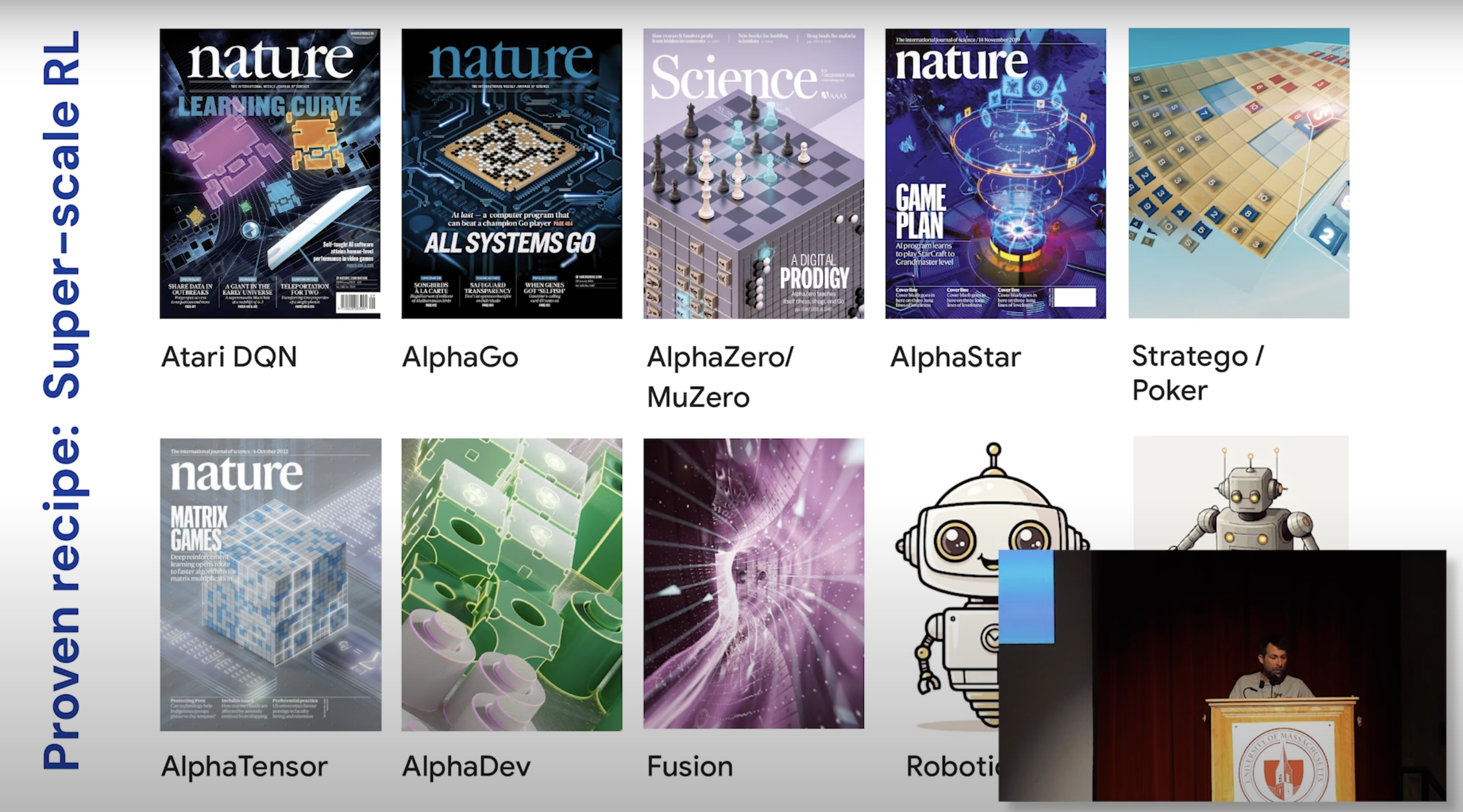
RL + Perfect Simulators + Compute = Superhuman

David Silver, RL Conference 2024

RL + Learned Simulators + Compute = Meh?

• In the absence of a perfect simulator, we can learn one from data

• In practice, this means collecting data from our problem’s environment, and building a model that simulates its dynamics

• But these models will only ever approximate the environment’s dynamics

- Finite data

- Function approximation

• So, a discrepancy between the dynamics modelled by learned simulators and the dynamics of the problem environment is inevitable

The Case for Zero-Shot RL

• Zero-shot RL methods aim to handle this discrepancy quickly

• Impressive progress has been made if the gap between the learned simulator and the real-world is small

• I contend that to solve real-world problems these methods need to deal with a larger gap and satisfy:

Chapter 3:
Zero-shot RL from Low Quality Data

Chapter 3: Zero-shot RL from Low Quality Data

Motivation

• The standard zero-shot RL methods, forward-backward representations (FB) [2] and universal successor features (USF) [3], provide principled mechanisms for performing zero-shot task generalisation

• However, they assume access to idealised (large & diverse) pre-training datasets that we can’t expect for real problems

• Can we pre-train zero-shot RL methods on realistic (small & narrow) datasets?

Scott Jeen, Tom Bewley, and Jonathan M. Cullen. Zero-shot Reinforcement Learning from Low Quality Data. In Advances in Neural Information Processing Systems 38, 2024

Chapter 3: Zero-shot RL from Low Quality Data

Failure mode: out-of-distribution value overestimation [4]

Chapter 3: Zero-shot RL from Low Quality Data

Failure mode: out-of-distribution value overestimation [4]

Chapter 3: Zero-shot RL from Low Quality Data

Failure mode: out-of-distribution value overestimation [4]

Chapter 3: Zero-shot RL from Low Quality Data

Conservative Zero-shot RL

Chapter 3: Zero-shot RL from Low Quality Data

Conservative Zero-shot RL

Chapter 3: Zero-shot RL from Low Quality Data

Conservative Zero-shot RL

Chapter 3: Zero-shot RL from Low Quality Data

Conservative Zero-shot RL

Chapter 3: Zero-shot RL from Low Quality Data

Conservative Zero-shot RL

C.f. [5]

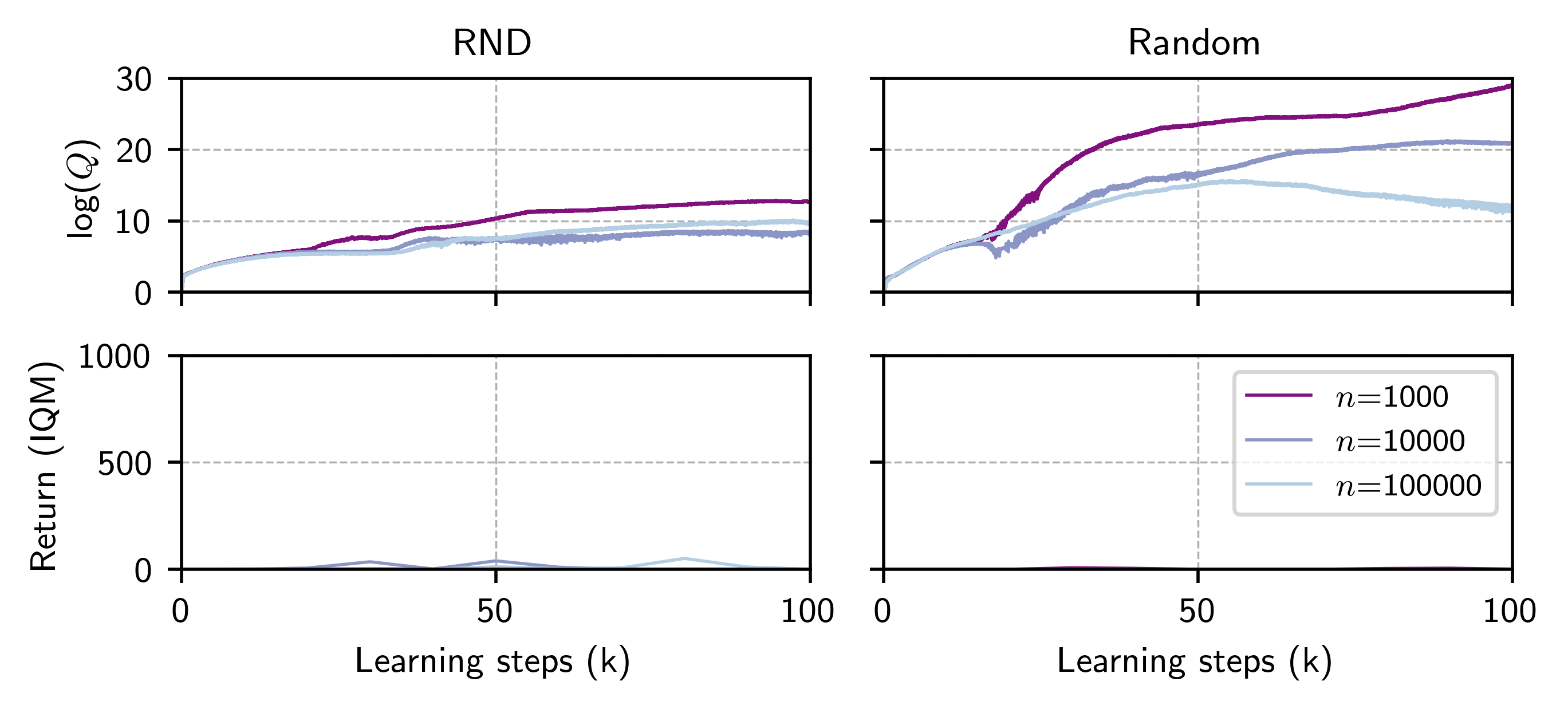
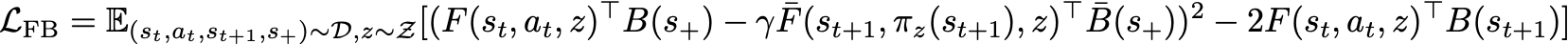
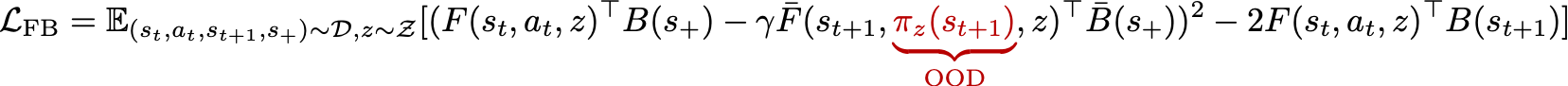
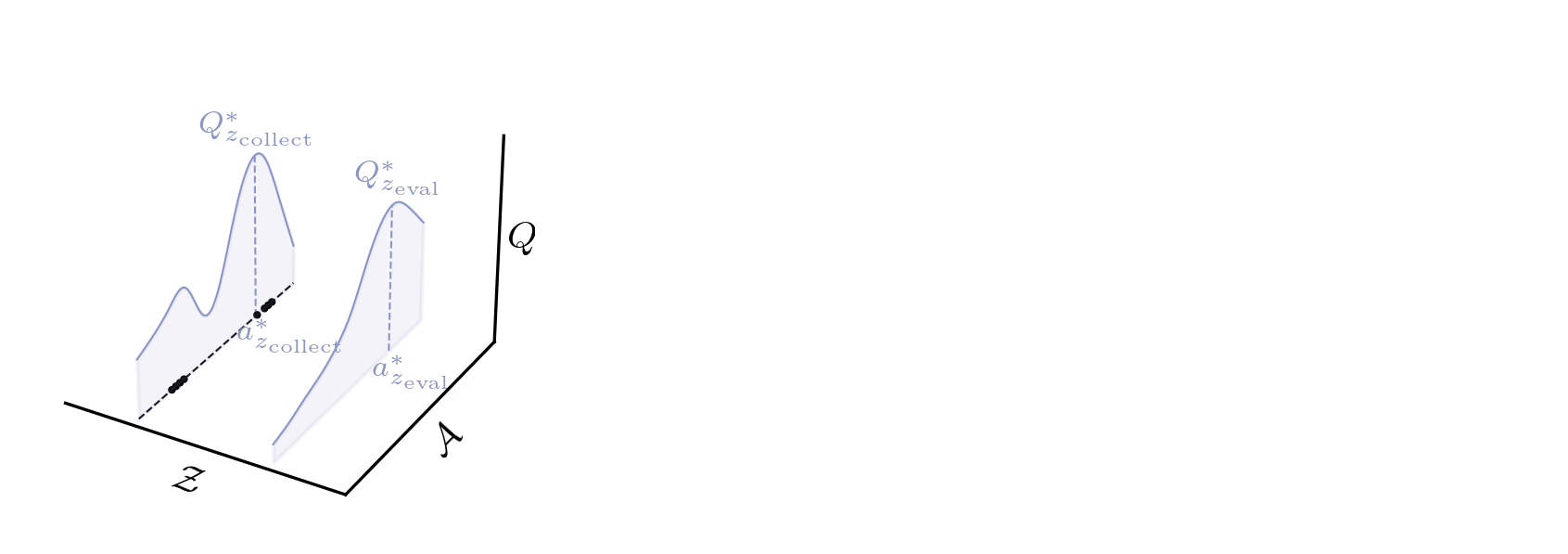
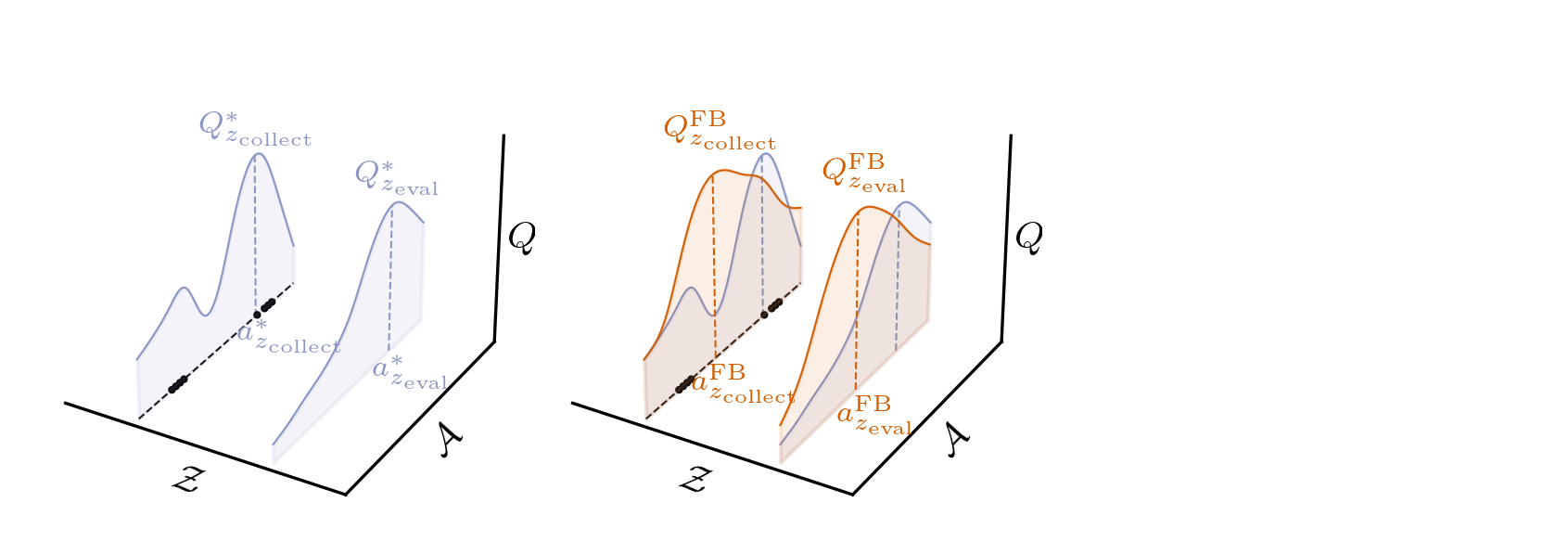
Chapter 3: Zero-shot RL from Low Quality Data

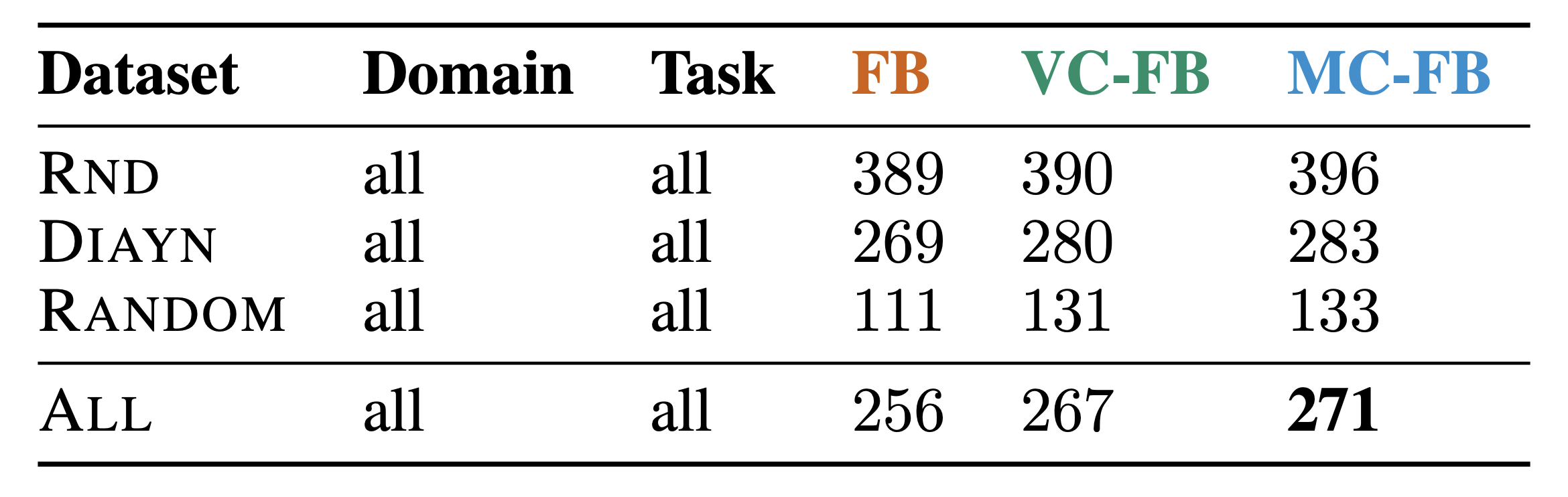
ExORL Experiments

Baselines

• Zero-shot RL: FB [2], SF-LAP [6]
• Goal-conditioned RL: GC-IQL [7]
• Offline RL: CQL [5]

Datasets

Chapter 3: Zero-shot RL from Low Quality Data

ExORL Results

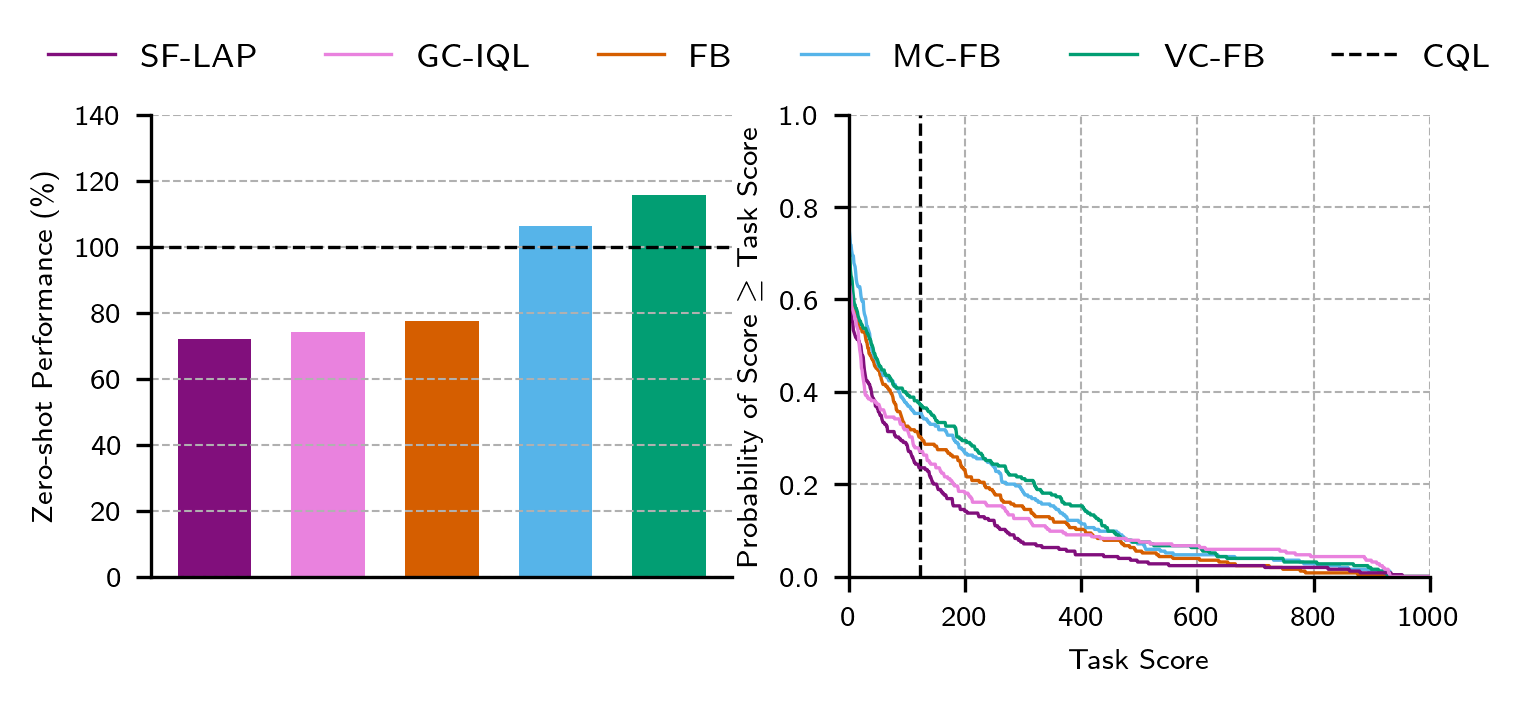
Chapter 3: Zero-shot RL from Low Quality Data

D4RL Results

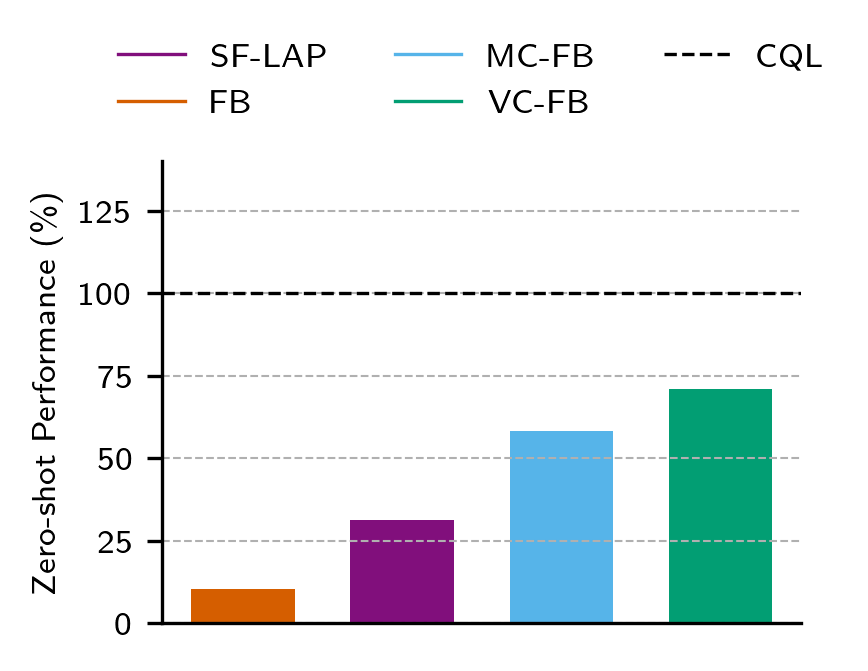
Chapter 3: Zero-shot RL from Low Quality Data

Performance on Idealised Datasets is Unaffected

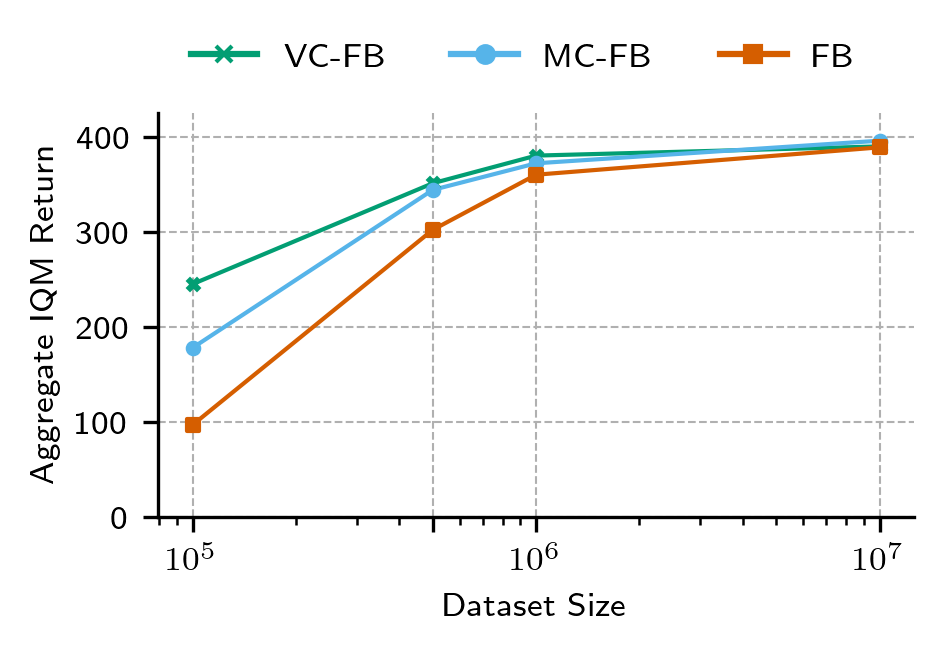
Chapter 3: Zero-shot RL from Low Quality Data

Conclusions

• Like standard offline RL methods, zero-shot RL methods suffer from the distribution shift

• As a resolution, we introduce conservative zero-shot RL methods

• Conservative zero-shot RL methods considerably outperform standard zero-shot RL methods on low-quality datasets

• Conservative zero-shot RL methods do not compromise performance on idealised datasets

Chapter 4:
Zero-shot RL under Partial Observability

Chapter 4: Zero-shot RL under Partial Observability

Motivation

• The standard zero-shot RL methods assume the assume the environment is fully observed.

• In many real-world problems the state is partially observed. Indeed, many other important problems in RL are naturally formulated as partially observed MDPs e.g. generalisation, temporal credit assignment etc.

• Can we pre-train zero-shot RL methods to perform well under partial observability?

Scott Jeen, Tom Bewley, and Jonathan M. Cullen. Zero-shot Reinforcement Learning Under Partial Observability.

Chapter 4: Zero-shot RL under Partial Observability

Failure mode: state and task mis-identification

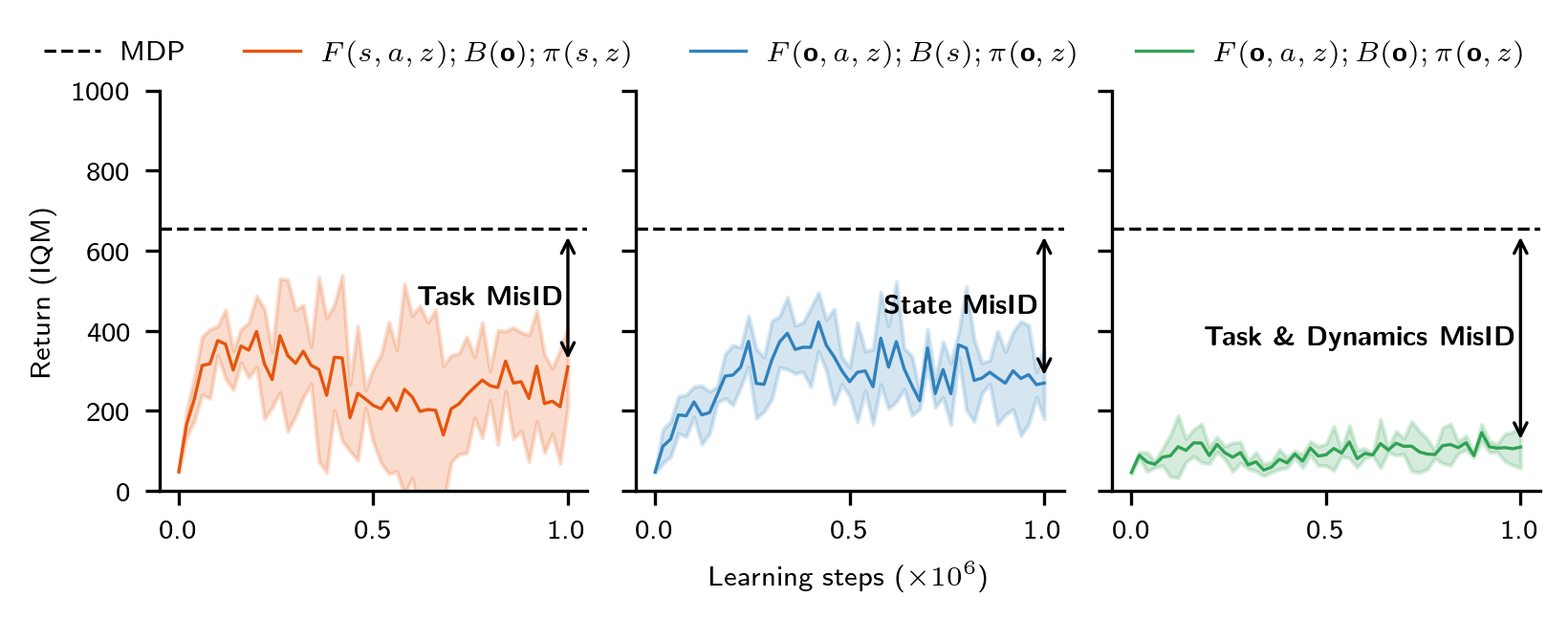
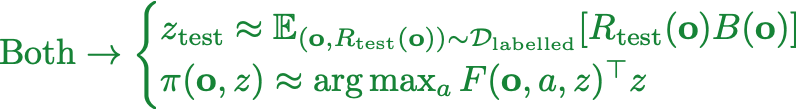
Chapter 4: Zero-shot RL under Partial Observability

Memory-based Zero-shot RL methods

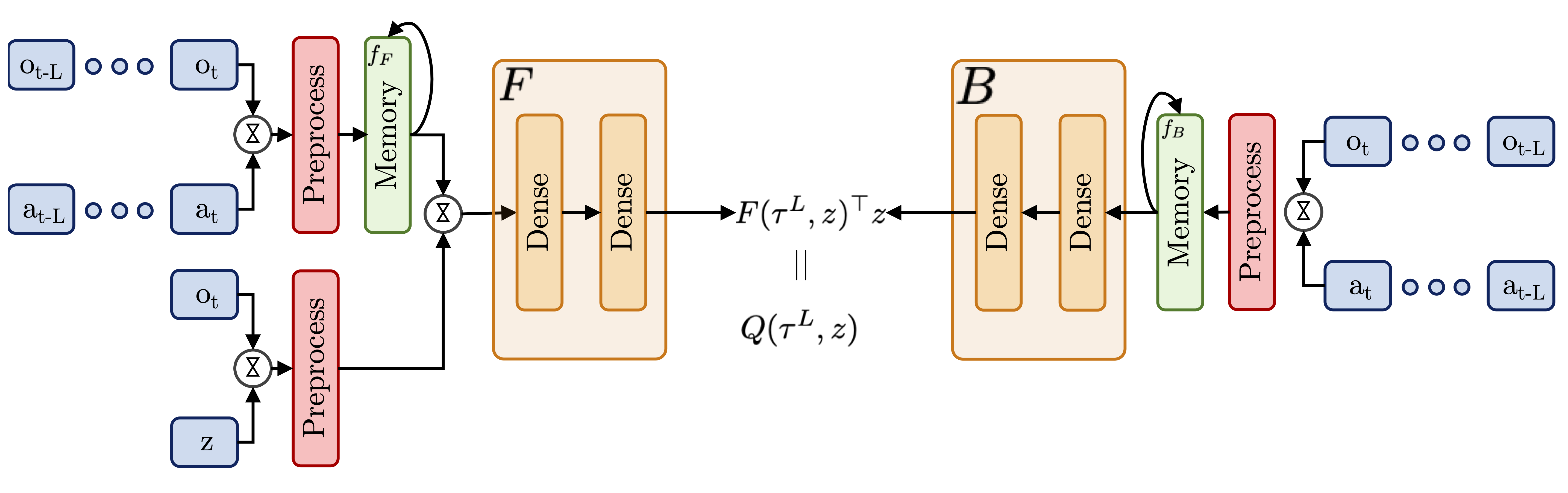
Chapter 4: Zero-shot RL under Partial Observability

ExORL Experiments

Baselines

• Zero-shot RL: FB [2], HILP [6], FB-stack
• Oracle: FB-MDP

Tests

• Standard POMDP: Noisey ExORL
• Generalisation: ExORL with dynamics interp./extrap.

Chapter 4: Zero-shot RL under Partial Observability

Standard POMDPs

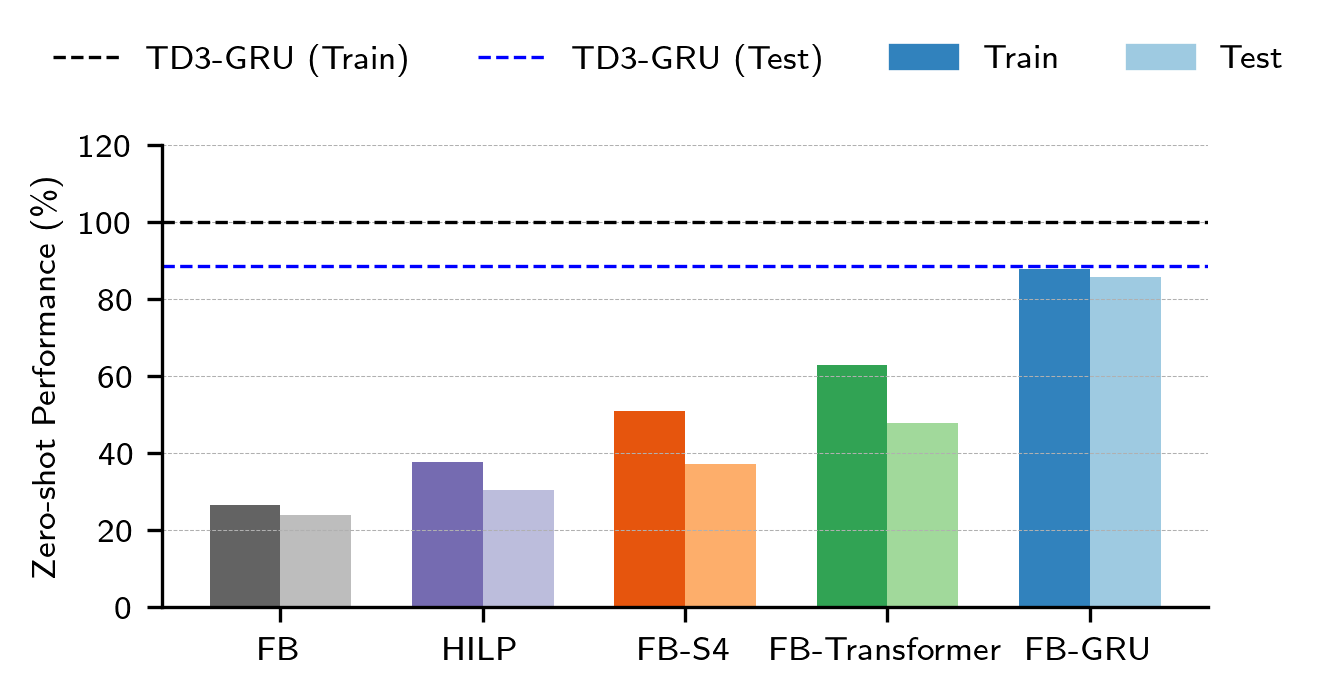
Chapter 4: Zero-shot RL under Partial Observability

Generalisation

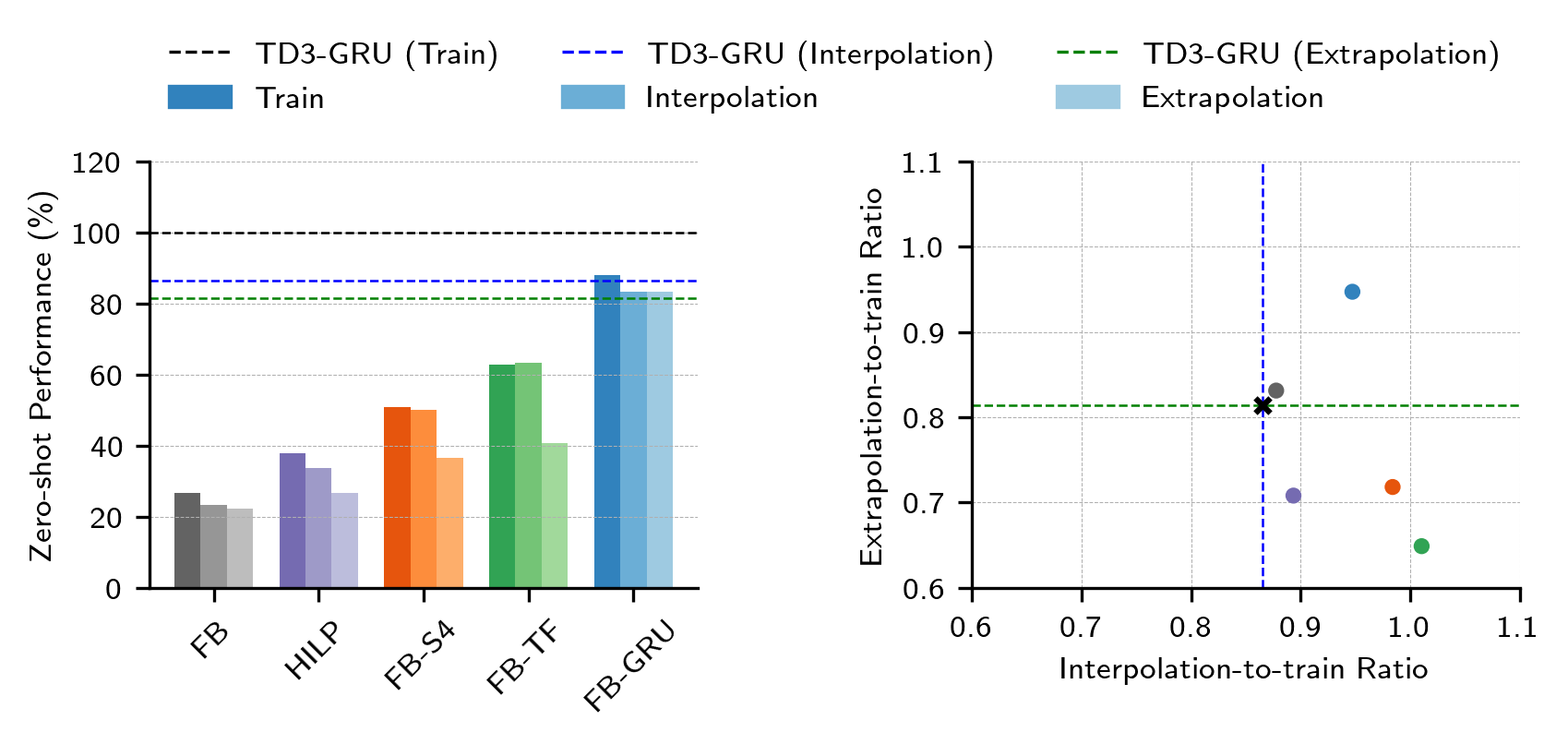
Chapter 4: Zero-shot RL under Partial Observability

Conclusions

• Real-world problems are often partially observed, yet zero-shot RL methods cannot handle partial observability out-of-the-box

• As a resolution, we introduce memory-based zero-shot RL methods

• Memory based zero-shot RL methods considerably outperform vanilla zero-shot RL methods on standard POMDPs, and show improved performance in the generalisation setting

Chapter 5: Zero-shot RL with No Prior Data

Chapter 5: Zero-shot RL with No Prior Data

Motivation

• For many real-world problems we have access to neither a simulator nor historical data logs.

• Emission-efficient building control is one such problem. But all prior works have assumed simulators or historical data logs are available.

• Can we learn to safely/efficiently control energy-intensive equipment in buildings online without any prior data?

Scott Jeen, Alessandro Abate, and Jonathan M. Cullen. Low Emission Building Control with Zero-Shot Reinforcement Learning. AAAI 2023

Chapter 5: Zero-shot RL with No Prior Data

Low Emission Building Control

Chapter 5: Zero-shot RL with No Prior Data

Low Emission Building Control

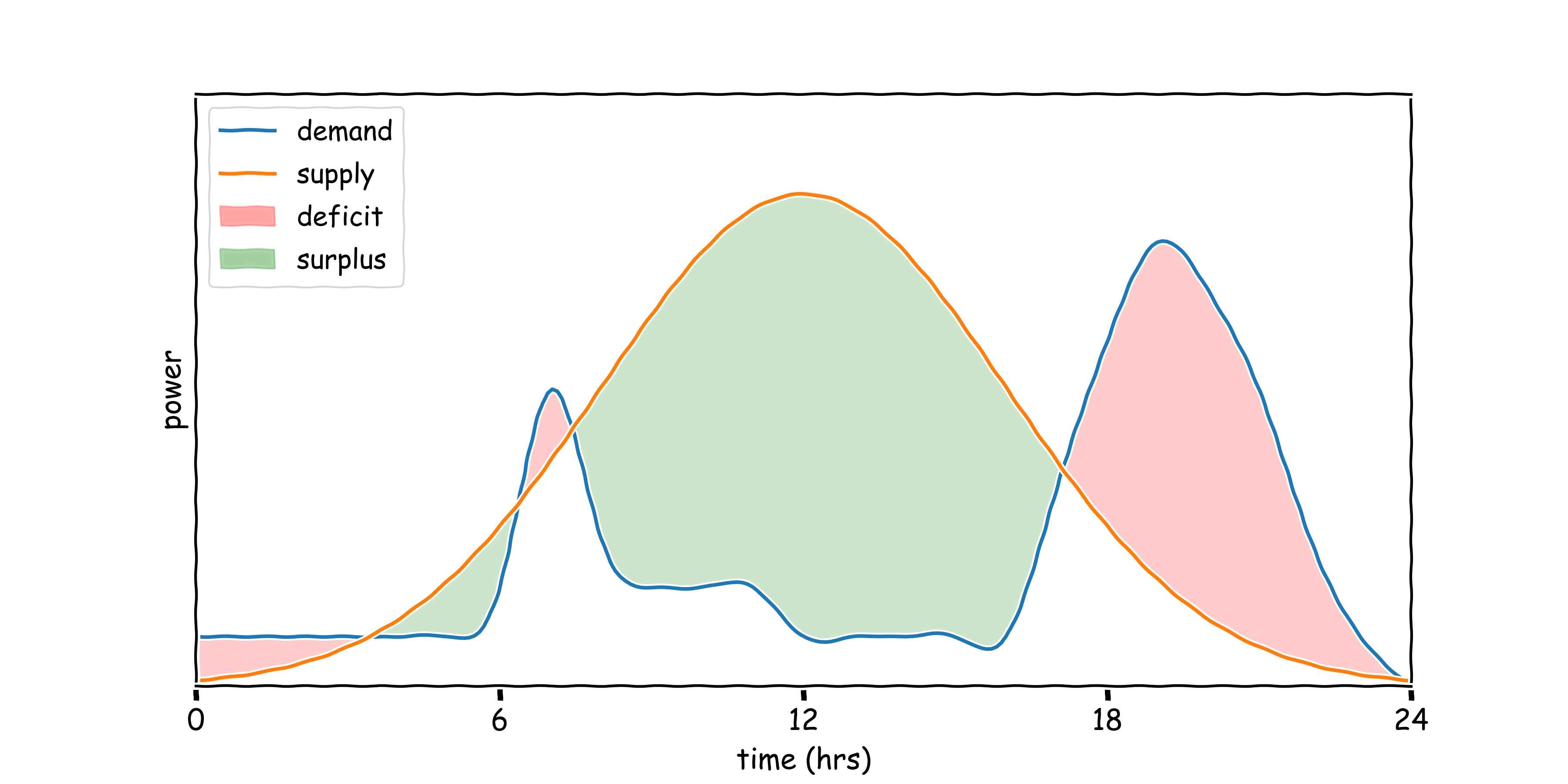
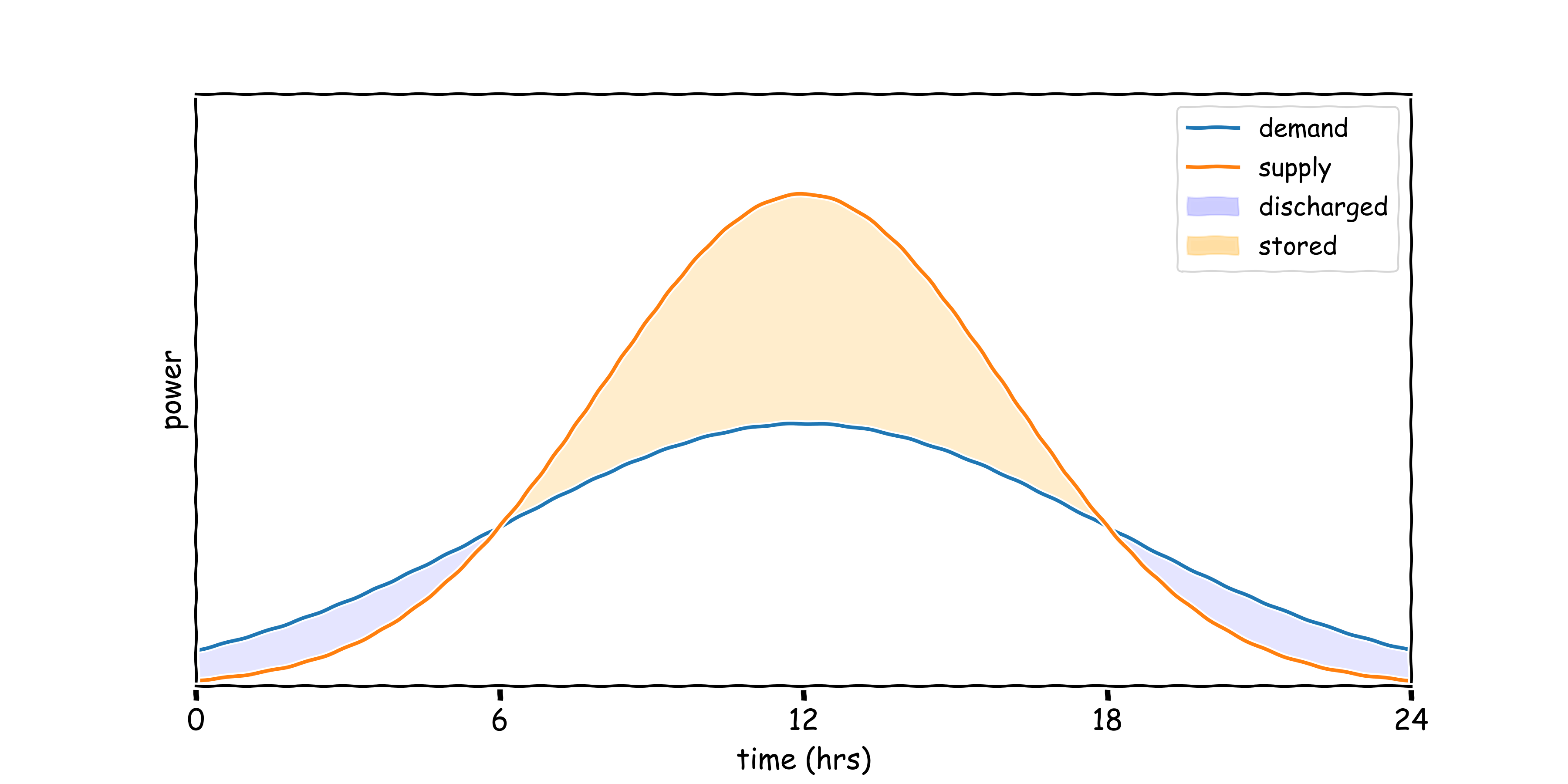
Chapter 5: Zero-shot RL with No Prior Data

Failure Mode of Existing Methods: Data (In)efficiency

       

Authors	Building	Algo	Efficiency	Data
Wei et al. (2017) [9]	5-zone Building	DQN	~35%	~8 years
Zhang et al. (2019) [10]	Office	A3C	~17%	~30 years
Valladares et al. (2019) [11]	Classroom	DQN	5%	~10 years

Chapter 5: Zero-shot RL with No Prior Data

PEARL: Probabilistic Emission Abating Reinforcement Learning

Chapter 5: Zero-shot RL with No Prior Data

Energym Experiments

Environments [15]

	Mixed-Use	Offices	Seminar Centre
Location	Greece	Greece	Denmark
Floor Area (m\(^2\))	566	643	1278
Action-space dim	\(\mathbb{R}^{12}\)	\(\mathbb{R}^{14}\)	\(\mathbb{R}^{18}\)
State-space dim	\(\mathbb{R}^{37}\)	\(\mathbb{R}^{56}\)	\(\mathbb{R}^{59}\)
Equipment	Thermostats & AHU Flowrates	Thermostats	Thermostats

Baselines

• SAC [12]
• PPO [13]
• MPC-DNN [14]
• RBC (a generic controller)

Chapter 5: Zero-shot RL with No Prior Data

Energym Results

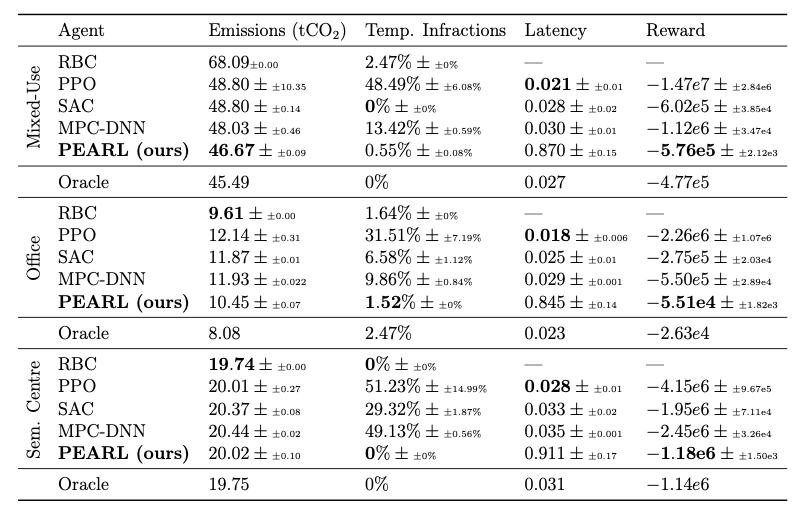
Chapter 5: Zero-shot RL with No Prior Data

System Identification

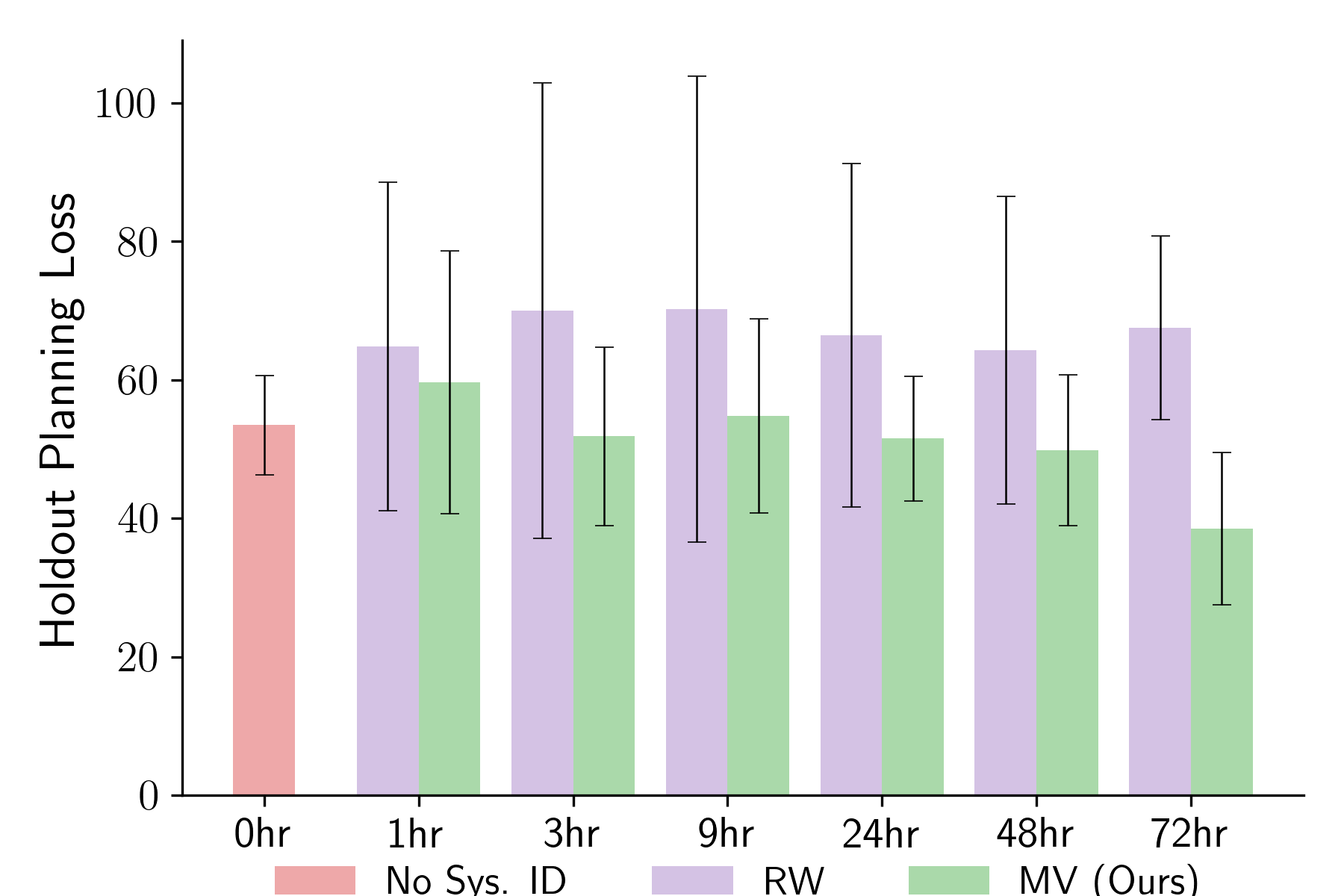
Chapter 5: Zero-shot RL with No Prior Data

Conclusions

• Standard deep RL methods are too data inefficient to be deployed for zero-shot building control

• We introduce PEARL, a method that can be deployed for zero-shot for building control

• PEARL outperforms the RBC in 1/3 environments and standard deep RL method in all environments

Conclusions

Conclusions

I set out to defend the following thesis:

• In Chapter 3, I took steps toward addressing the data quality constraint with conservative zero-shot RL methods

• In Chapter 4, I took steps toward addressing the observability constraint with memory-based zero-shot RL methods

• In Chapter 5, I took steps to addressing the data availability constraint (in the context of buidling control) with PEARL

Looking forward to the discussion!

References

[1] Sutton, R. and Barto, A. (2018). Reinforcement Learning: An Introduction. The MIT Press, second edition.

[2] Touati, A. and Ollivier, Y. (2021). Learning one representation to optimize all rewards. Advances in Neural Information Processing Systems, 34:13–23

[3] Borsa, D., Barreto, A., Quan, J., Mankowitz, D., Munos, R., Van Hasselt, H., Silver, D., and Schaul, T. (2018). Universal successor features approximators. arXiv preprint arXiv:1812.07626.

[4] Kumar, A., Fu, J., Soh, M., Tucker, G., and Levine, S. (2019). Stabilizing off-policy q-learning via bootstrapping error reduction. In Advances in Neural Information Processing Systems, volume 32

[5] Kumar, A., Zhou, A., Tucker, G., and Levine, S. (2020). Conservative q-learning for offline reinforcement learning. arXiv preprint arXiv:2006.04779.

[6] Touati, A., Rapin, J., and Ollivier, Y. (2023). Does zero-shot reinforce- ment learning exist? In The Eleventh International Conference on Learning Representations.

[7] Park, S., Ghosh, D., Eysenbach, B., and Levine, S. (2023). Hiql: Offline goal- conditioned rl with latent states as actions. Advances in Neural Information Processing Systems, 37.

[8] Park, S., Kreiman, T., and Levine, S. (2024). Foundation policies with hilbert representations. International Conference on Machine Learning.

[9] Wei, T., Wang, Y., and Zhu, Q. (2017). Deep reinforcement learning for building hvac control. In Proceedings of the 54th Annual Design Automation Conference 2017, DAC ’17, New York, NY, USA. Association for Computing Machinery.

[10] Zhang, Z., Chong, A., Pan, Y., Zhang, C., and Lam, K. P. (2019b). Whole building energy model for hvac optimal control: A practical framework based on deep reinforcement learning. Energy and Buildings, 199:472–490.

[11] Valladares, W., Galindo, M., Gutiérrez, J., Wu, W.-C., Liao, K.-K., Liao, J.-C., Lu, K.-C., and Wang, C.-C. (2019). Energy optimization associated with thermal comfort and indoor air control via a deep reinforcement learning algorithm. Building and Environment, 155:105 – 117.

[12] Haarnoja, T., Ha, S., Zhou, A., Tan, J., Tucker, G., and Levine, S. (2018a). Learning to walk via deep reinforcement learning. arXiv preprint arXiv:1812.11103.

[13] Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and Klimov, O. (2017). Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347.

[14] Nagabandi, A., Kahn, G., Fearing, R. S., and Levine, S. (2018c). Neural network dynamics for model-based deep reinforcement learning with model- free fine-tuning. In 2018 IEEE International Conference on Robotics and Automation (ICRA), pages 7559–7566. IEEE.

[15] Scharnhorst, P., Schubnel, B., Fernández Bandera, C., Salom, J., Taddeo, P., Boegli, M., Gorecki, T., Stauffer, Y., Peppas, A., and Politi, C. (2021). Energym: A building model library for controller benchmarking. Applied Sciences, 11(8):3518.