Searching for useful problems

This post is based on a talk I gave to my research group at Cambridge University in June 2024. You can find the notes and slides for the talk here.

Solutions to most problems aren’t particularly useful. Solutions to a small number of problems are extremely useful. If you’re interested in doing good, you’ll want to search for problems that look like the latter. It’s a hard search, but the ROI is likely greater than any other use of your time, and I have some ways of running it that I think make it a little more tractable.

A solution to a problem provides some gain in exchange for some cost. Less useful problems are those whose solutions incur costs that are equal to or higher than the expected gains. Useful problems are those whose solutions provide gains that greatly outweigh the costs. The former are zero-sum games, and the latter are positive-sum games. Chess is the canonical zero-sum game: every gain in the position of Player A is a loss in the position of Player B. Trade is the canonical positive-sum game: when countries specialise in products they make most cheaply, and trade them for those they make less cheaply, both benefit. Maximising good necessitates working on problems with positive-sum solutions. Indeed, your goal should be to find problems whose solutions are maximally positive-sum.

Identifying these problems is difficult for two reasons: 1) it’s hard to predict expected gain, and 2) it’s hard to predict expected cost (relative to the cost incurred by others working on the same problem¹). Below I discuss methods for dealing with each.

Moral axioms and proxies (or evaluating the expected gain from a solved problem)

Finding problems with solutions that maximise expected gain means knowing what you’d like to gain. It’s easy to convince yourself that you know this already, but, often, what you think you’d like to gain only approximates a more deeply held belief. You’ll know you’ve found these beliefs when they feel axiomatic, like unchallengeable truths for which you don’t need to provide justification. One might be that maximising net happiness is a good thing. Another might be that fulfilling the desires of the maximum number of people is a good thing. To maximise expected gain, you’ll want to solve problems that contribute to these moral axioms as much as possible².

Your moral axioms are problems that you can’t access directly (I can’t click my fingers and make everyone happier). Instead, you access them through proxies—problems that, if solved, partially contribute to your moral axiom. These proxies will have their own sub-problems with solutions that partially contribute to their solution. Each moral axiom has an associated tree of proxies, as in Figure 1.

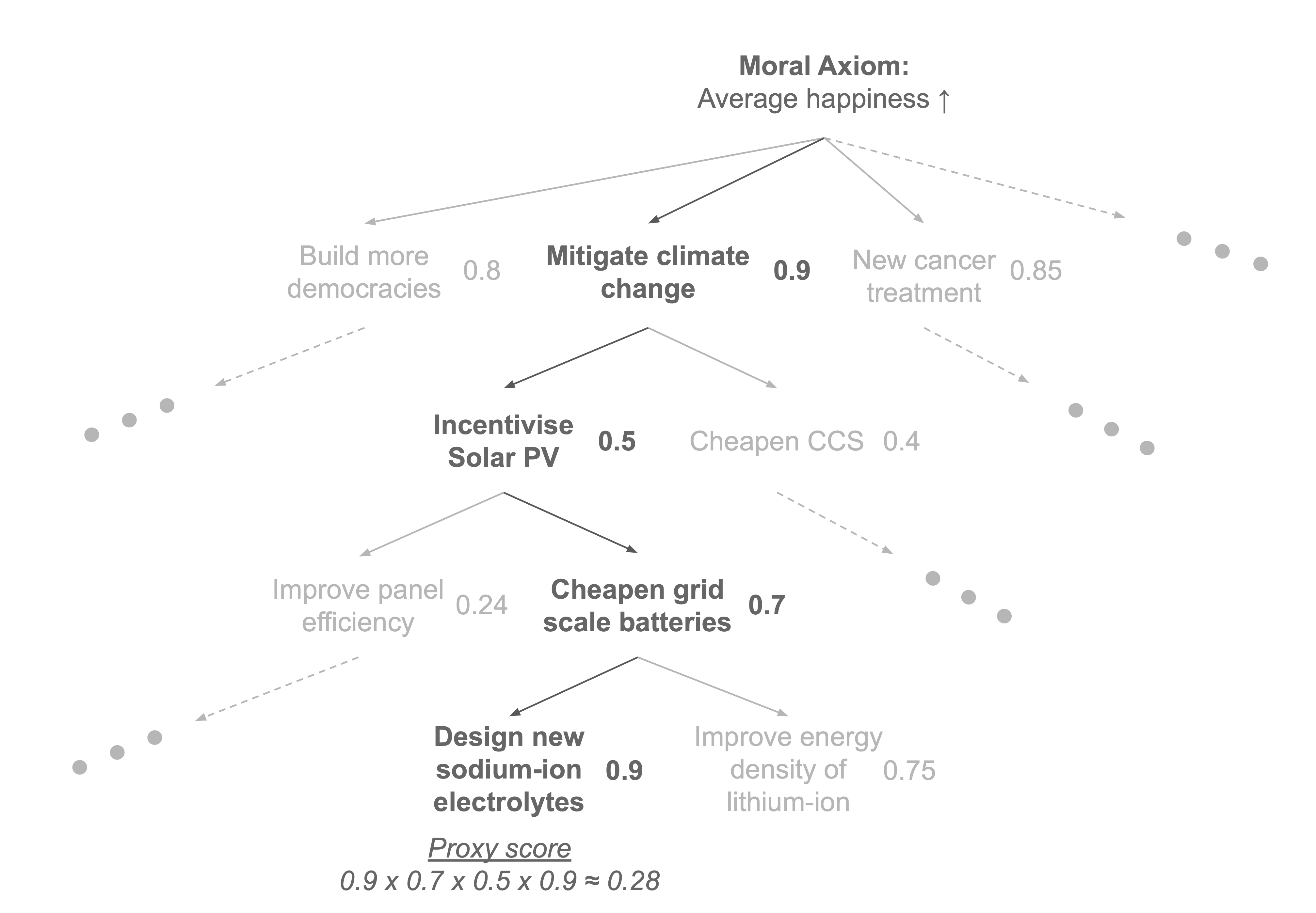
Figure 1. Moral axioms and proxies. Starting with a moral axiom (a moral belief that requires no justification) we build a tree of sub-problems or proxies. Each proxy has a solution which part-solves the proxy from the previous level in the tree. The degree to which the previous proxy is solved by the current proxy is approximated by its value (a number between 0 and 1). For a given proxy, its expected value or proxy score with respect to the moral axiom is found by multiplying each of the values you traverse to find it in the tree.

Proxies contribute to other proxies to different degrees. In Figure 1, I consider incentivising solar PV as a proxy for mitigating climate change, which is itself a proxy for increasing average happiness. I provide two solutions: a) new panels with improved conversion efficiency, or b) cheaper (i.e. more) grid scale batteries which allow generators to reliably sell excess energy to the grid. Here, I assume reliable income for surplus energy better incentivises solar PV than improved panel efficiency, so b) contributes more to the proxy than a). These contributions are summarised by their value with respect to the proxy above—a number between 0 and 1, where 0 represents no contribution and 1 constitutes a full solution to the problem. The expected value, or proxy score, of a solution with respect to the moral axiom is found by multiplying each of the values you traverse to find it in the tree. It’s called the proxy score because it measures how well the problem approximates the real problem you want solve i.e. your moral axiom. Proxies are ranked using these scores.

Building the ground truth tree of proxies and values for a given moral axiom is clearly intractable. The best you can do is create as exhaustive a list of proxies as you can, and score them to the best of your current knowledge. What’s nice, however, is that building this tree is a lifelong project, and the tree can always be improved. As you learn more, you’ll identify new proxies and score them, or refine scores for old proxies, which will re-rank them. The trick is being willing to switch proxies when your ranking updates.

Being the (Pareto) best in the world (or evaluating the expected cost of solving a problem)

If you are the best in the world at something you are uniquely positioned to solve its problems cheaply. Usain Bolt’s training and physique meant he was uniquely capable of running the 100m faster than anyone who came before. Marie Curie’s knowledge of radioactivity meant she was uniquely capable of proposing radiation therapy as a form of cancer treatment. But being the best in the world at something is hard. It is much easier to be the best in the world at a combination of things.

In the simplest case you can think about how you compare to others at a combination of two skills, as in Figure 2. Here, people are plotted with respect to their gardening and public speaking skill. I assume Mandela is history’s best public speaker and (for simplicity) knows nothing of gardening, and vice versa for Alan Titchmarsh. Between lie three people, Jane, Julia and John, each of whom have differing combined skills. Together these five make a Pareto front of gardening/public speaking knowledge.

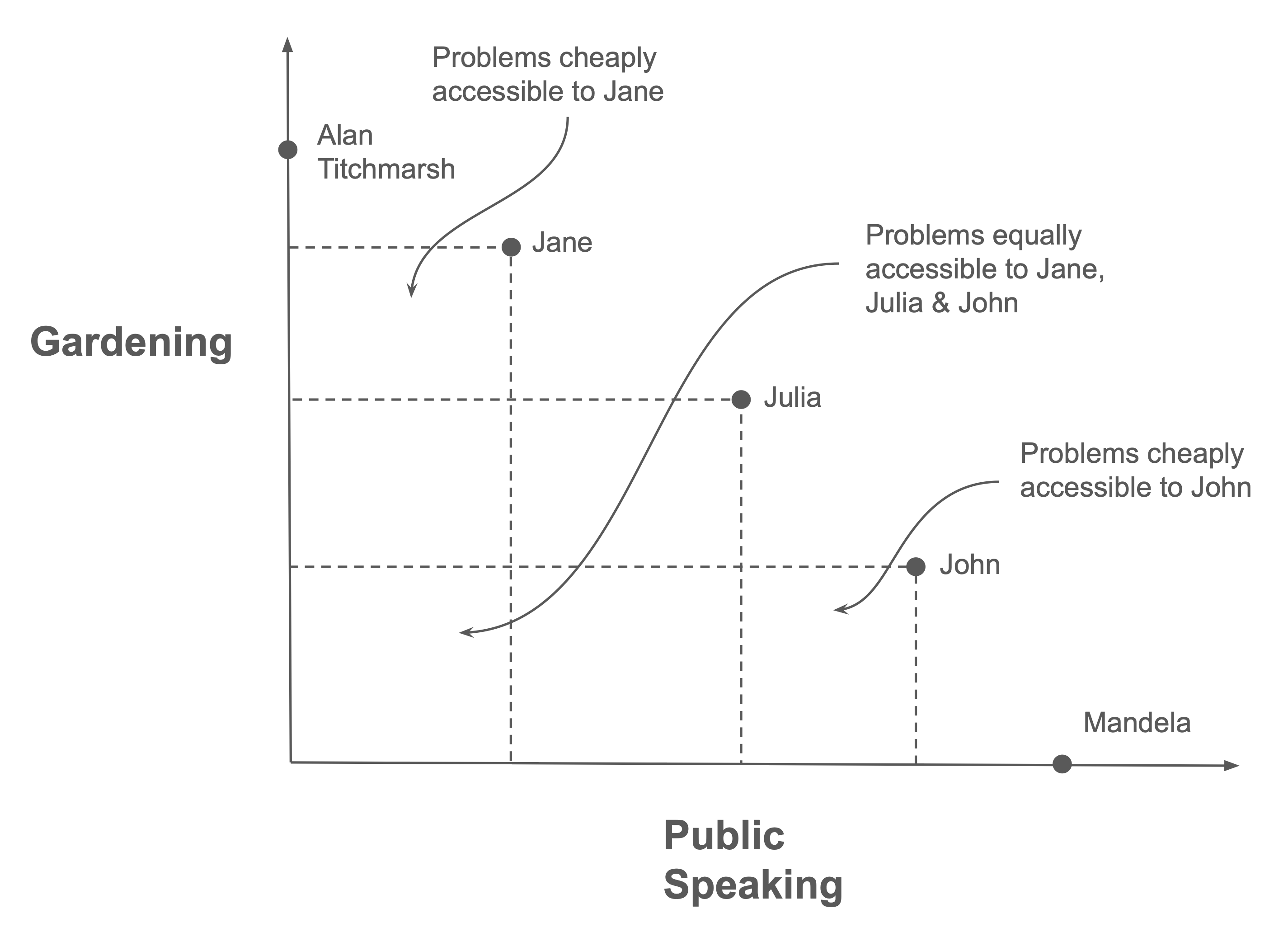
Figure 2. Being the (Pareto) best in the world³. Five people plotted with respect to their gardening and public speaking skill. Problems reveal themselves to each person depending on their unique combination of skills.

Each person’s position on the Pareto front illuminates problems that are cheaply accessible to them. The further some person is from their neighbours, the more problems they can access. In practice, it’s difficult to be the best in the world across the intersection of two skills, but you may find you are the best in the world across the intersection of three, four or five. There may be nobody in the world better than Julia at gardening, public speaking, Catalan, and rust programming. The limit case is the intersection of all of your skills, and at that you are definitively unmatched. There is nobody in the world better at being you than you.

Your position on the real Pareto skill front changes as you learn new skills. The number of new problems cheaply accessible to you is dependent on what these new skills are. If you are a native English speaker, extending your English vocabulary won’t differentiate you much from other fluent English speakers, and is unlikely to unlock new problems that you can’t currently access. Learning Estonian enters you to a much smaller cohort of English-Estonian speakers, and opens up some problems that are communicated only in Estonian.

Consider carefully what new skills would maximally differentiate you from your neighbours on the Pareto front, and learn them to increase the number of problems you can solve cheaply. The best skills to learn are those that illuminate problems with highest proxy score as established from your moral axioms and proxies.

Key takeaways

1. Think deeply about your moral axioms (beliefs that require no justification), and build a tree of proxies (sub-problems) and their values that is as exhaustive as possible.
2. Rank proxies by their proxy score (expected value).
3. Think about what combination of skills you are Pareto best at, and find the proxy with the highest score that requires these (i.e. for which you have a comparative advantage in solving).
4. Think about new skills that, if learned, would unlock proxies with higher proxy scores. Learn them.

Further reading

• Ofir Nachum’s Baselines and Oracles for checking that a solution exists to a given problem.
• Uri Alon’s How To Choose a Good Scientific Problem for other ways of thinking about problem usefulness and feasibility.