An introduction to black-box function approximators¶

Scott Jeen ¶

Xchange Seminar, 15th March 2021¶

Today's Talk¶

My project
Black-box function approximation
- Deterministic approach: Neural networks and Long-short term memory (LSTMs)
- Probabilistic approach: Gaussian processes (GPs)
Timeseries applications
Key takeaways

1. My Project¶

Video: Deepmind's Deep Q-network solving the Atari game Breakout after 600 episodes of self-play (Mnih et. al (2013))

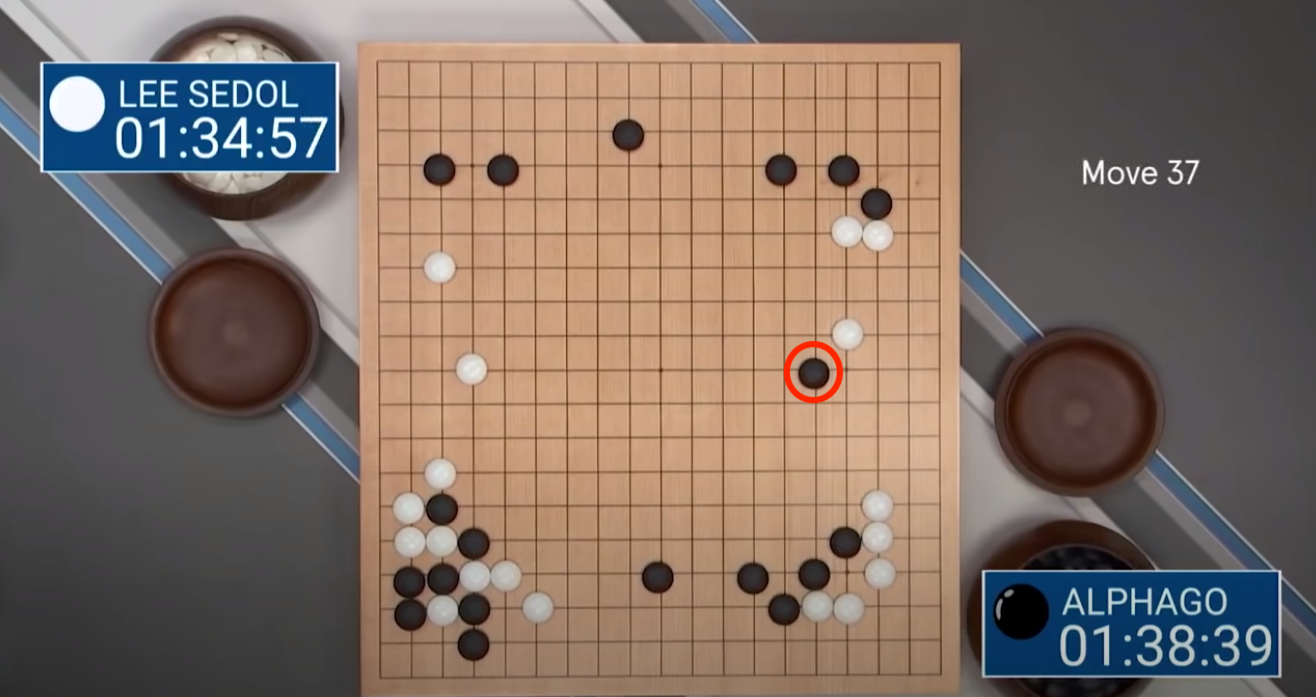
Figure: Top: AlphaGo's infamous Move 37, a counterintuitive move for a human to make with this board set-up, but nonetheless a gaming-winning one. Bottom: Lee Sedol, the world no.1 Go player, flumexed by AlphaGo's moves. (Silver et al (2017))

Figure: The complex, interconnected electricity grid

1.1 Reinforcement Learning¶

Figure: The RL control loop. Agent's take sequential actions that affect their environment, the environment changes and the agent receives a reward for their action. Adapted from Episode 1 of David Silver's RL Youtube series

More formally, the RL control loop looks something like this:

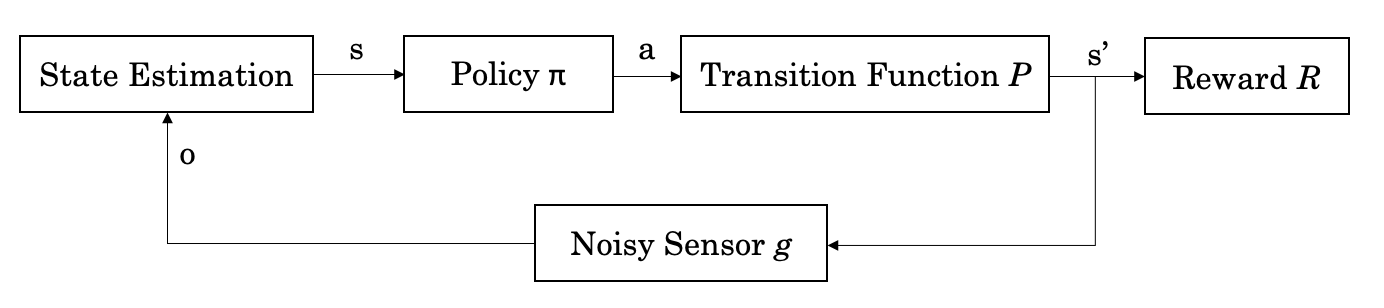
Figure: The formalised RL control loop.

2. Black-box Function Approximation¶

2.1 Two approaches to modelling¶

Generally when we model a function using a black-box approximator, we can select (informally) from two sets of models, these are:

Deterministic models: Do not contain elements of randomness; everytime the model is run with the same initial conditions it produces identical results.
Probabilistic models: Include elements of randomness; trials with identical initial conditions will produce different results.

2.2 Deterministic Models: Neural Networks¶

Linear Basis¶

$$ f(x) = {\color{red}{w_0}} + {\color{blue}{w_1} x} $$

In [15]:

from ipywidgets import interact
import ipywidgets as widgets

def y_linear_plot(w1, w0):
    
    y_lin = w1*x_true+w0
    y_err = w1*x+w0
    
    with plt.xkcd():
        fig = plt.figure(figsize=(10,5))
        plt.xlim([-6,6])
        plt.ylim([-4,4])
        plt.scatter(x, y, 100, 'k', 'o', zorder=100)
        plt.plot(x_true, y_lin)
        plt.vlines(x=x, ymin=y_err, ymax=y, colors='green', ls=':', lw=2)
        plt.savefig(path+'/images/2_data.png', dpi=300)
        plt.show()

interact(y_linear_plot, w1=widgets.FloatSlider(value=0.75, min=-5, max=5, step=0.25),
                    w0=widgets.FloatSlider(value=-.25, min=-5, max=5, step=0.25))

Out[15]:

<function __main__.y_linear_plot(w1, w0)>

Polynomial Basis¶

$$ f(x) = {\color{red}{w_0}} + {\color{blue}{w_1}} x + {\color{green}{w_2}} x^2 + {\color{orange}{w_3}} x^3 $$

In [16]:

def y_poly_plot(w0, w1, w2, w3):
    
    y_poly = w0 + w1*x_true + w2*(x_true**2) + w3*(x_true**3)
    y_polyerr = w0 + w1*x + w2*(x**2) + w3*(x**3)
    
    with plt.xkcd():
        fig = plt.figure(figsize=(10,5))
        plt.xlim([-6,6])
        plt.ylim([-4,4])
        plt.scatter(x, y, 100, 'k', 'o', zorder=100)
        plt.plot(x_true, y_poly)
        plt.vlines(x=x, ymin=y_polyerr, ymax=y, colors='green', ls=':', lw=2)
        plt.savefig(path+'/images/3_data.png', dpi=300)
        plt.show()

interact(y_poly_plot,
             w0=widgets.FloatSlider(value=-1, min=-7, max=7, step=0.5),
             w1=widgets.FloatSlider(value=-.5, min=-7, max=7, step=0.5),
             w2=widgets.FloatSlider(value=1.5, min=-7, max=7, step=0.5),
             w3=widgets.FloatSlider(value=1, min=-7, max=7, step=0.5),
        )

Out[16]:

<function __main__.y_poly_plot(w0, w1, w2, w3)>

Rectified Linear Unit (ReLU)¶

$$ f(x) = \max (0 , {\color{blue}{w_1}} x + {\color{red}{w_0}}) $$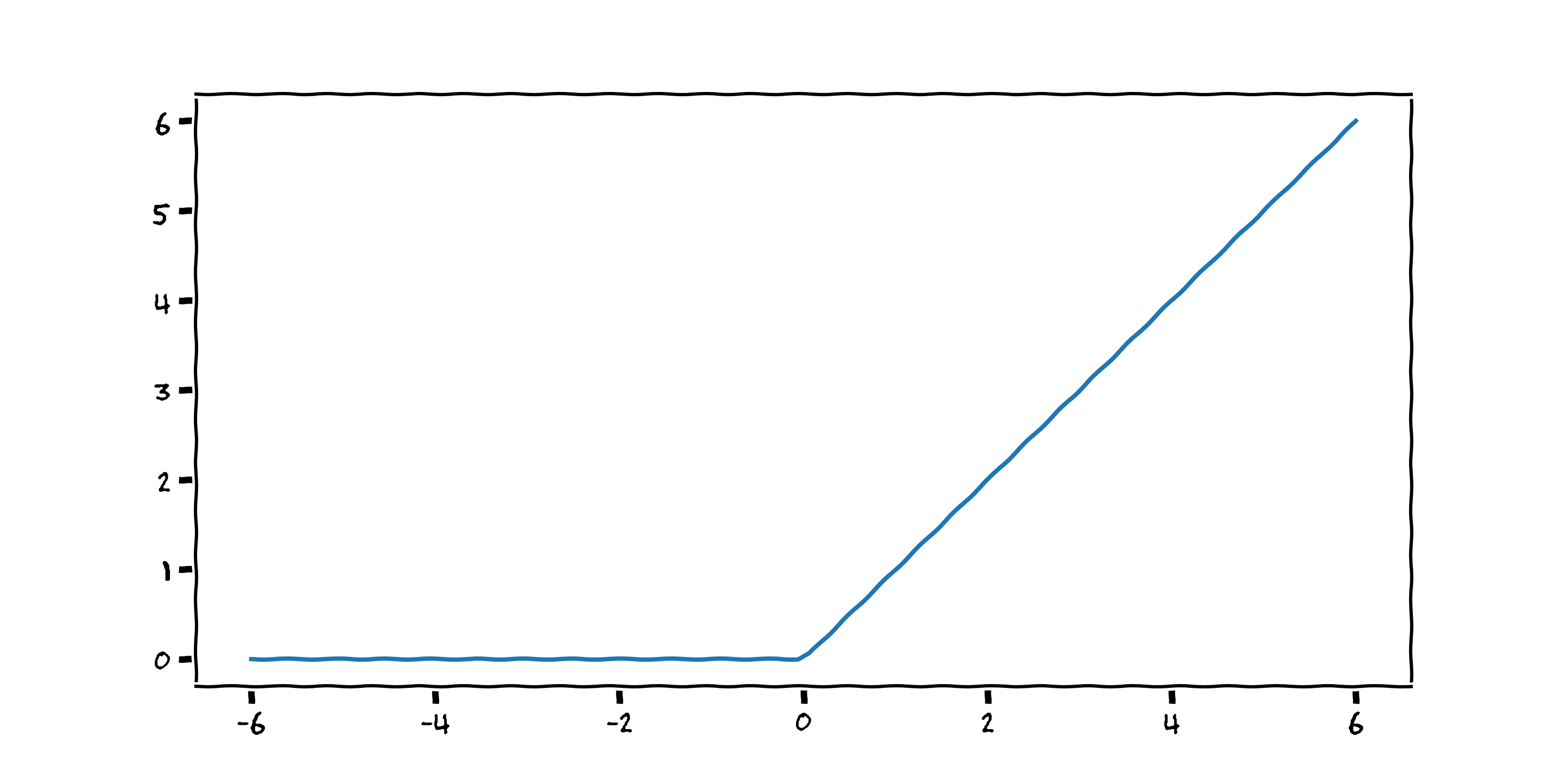

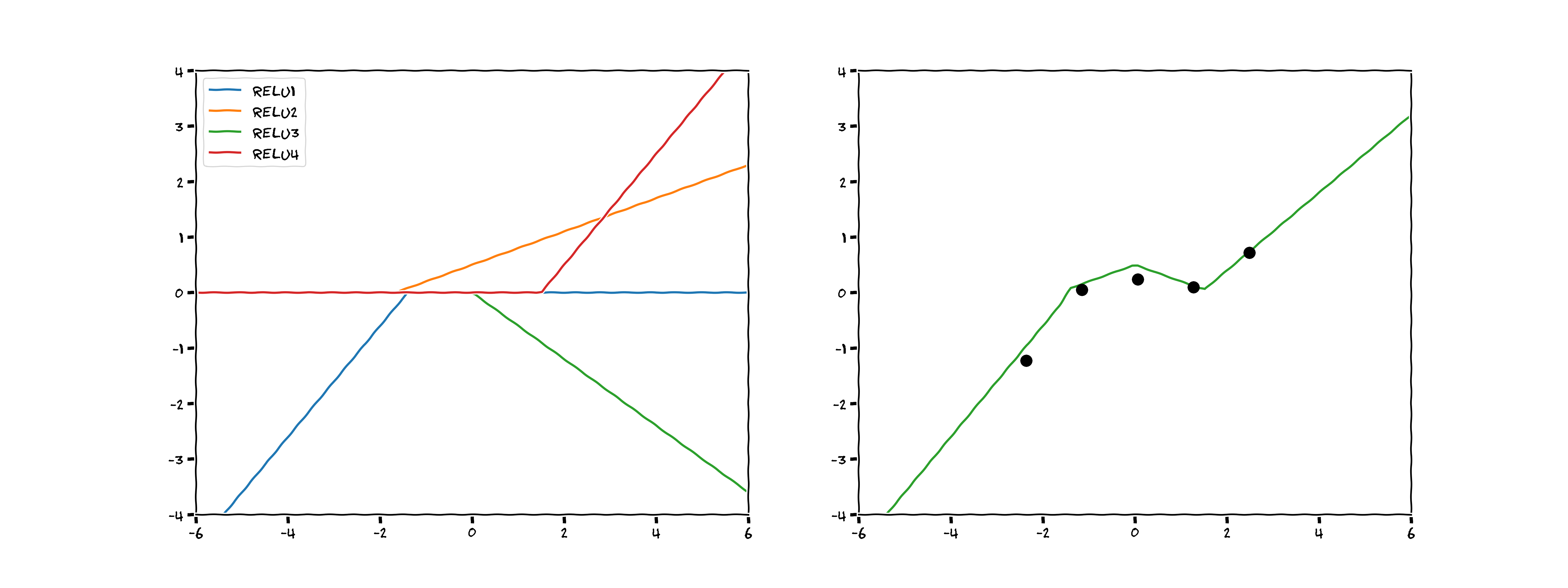
Figure: Top: A neural network with 4 nodes and 1 hidden layer–a graph of the model created by hand above. Bottom: A neural network with 10 nodes and 2 hidden layers–a more typical model arrangement.

3. Probabilistic Models: Gaussian Processes¶

We use Bayes' rule to narrow the solution space, which tells us how to update our beliefs about the world based on the evidence we've seen:

$$ P (A | B) = \frac{P(B | A) P(A)}{P(B)} $$

and in the setting of functions and data it looks something like:

$$ P (\textbf{f} | \textbf{D}) = \frac{P(\textbf{D} | \textbf{f}) P(\textbf{f})}{P(\textbf{D})} $$

In [24]:

# plot rbf kernel
with plt.xkcd():
    fig = plt.figure(figsize=(10,5))
    plt.scatter(x, y, 100, 'k', 'o', zorder=100)
    plt.plot(x_true, f_rbf.T)
    plt.xlim([-6,6])
    plt.ylim([-4,4])
    plt.savefig(path+'/images/8_data.png', dpi=300)
    plt.show()

3.1 Prior Beliefs¶

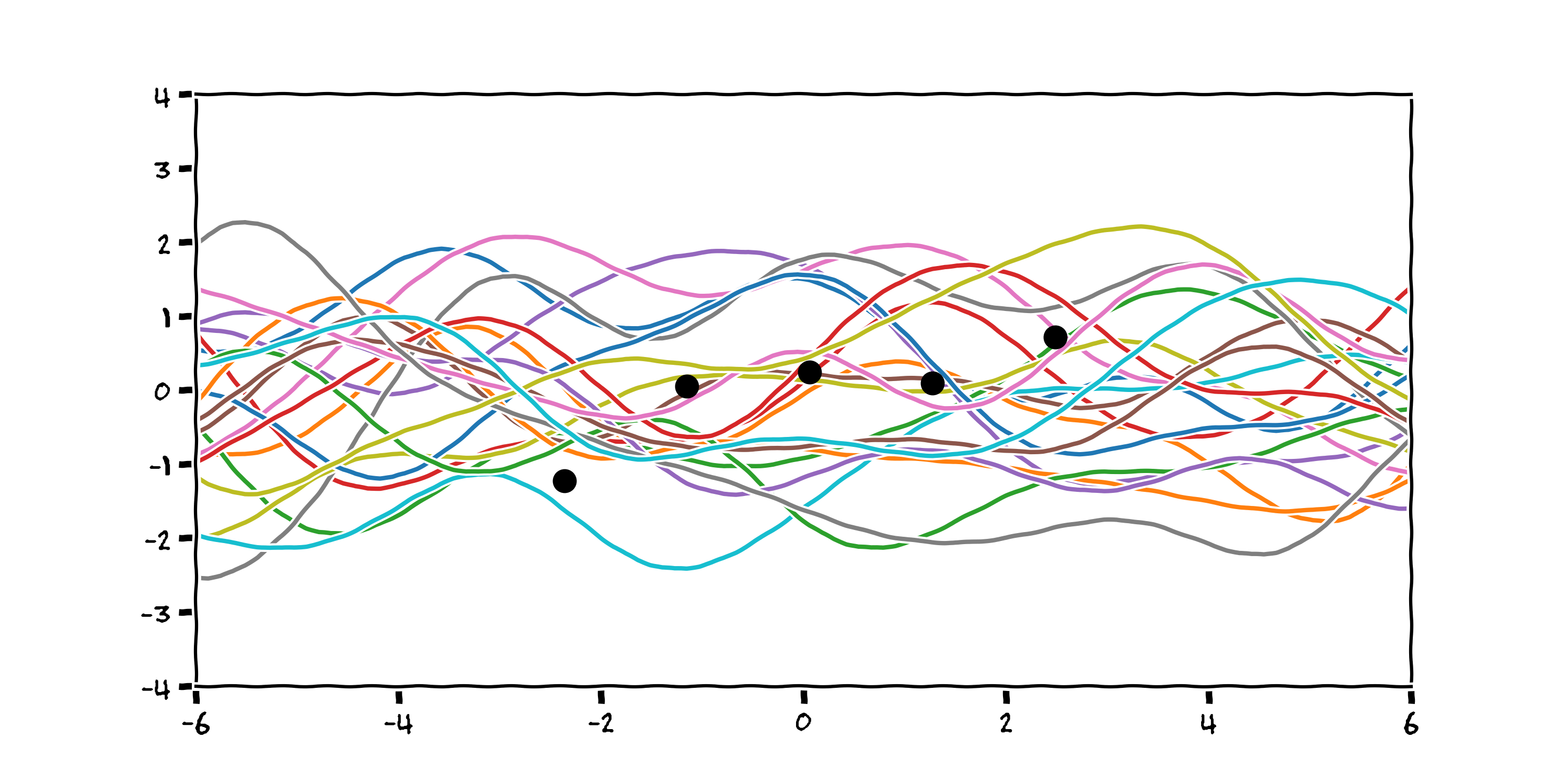
3.2 (Different) Prior Beliefs¶

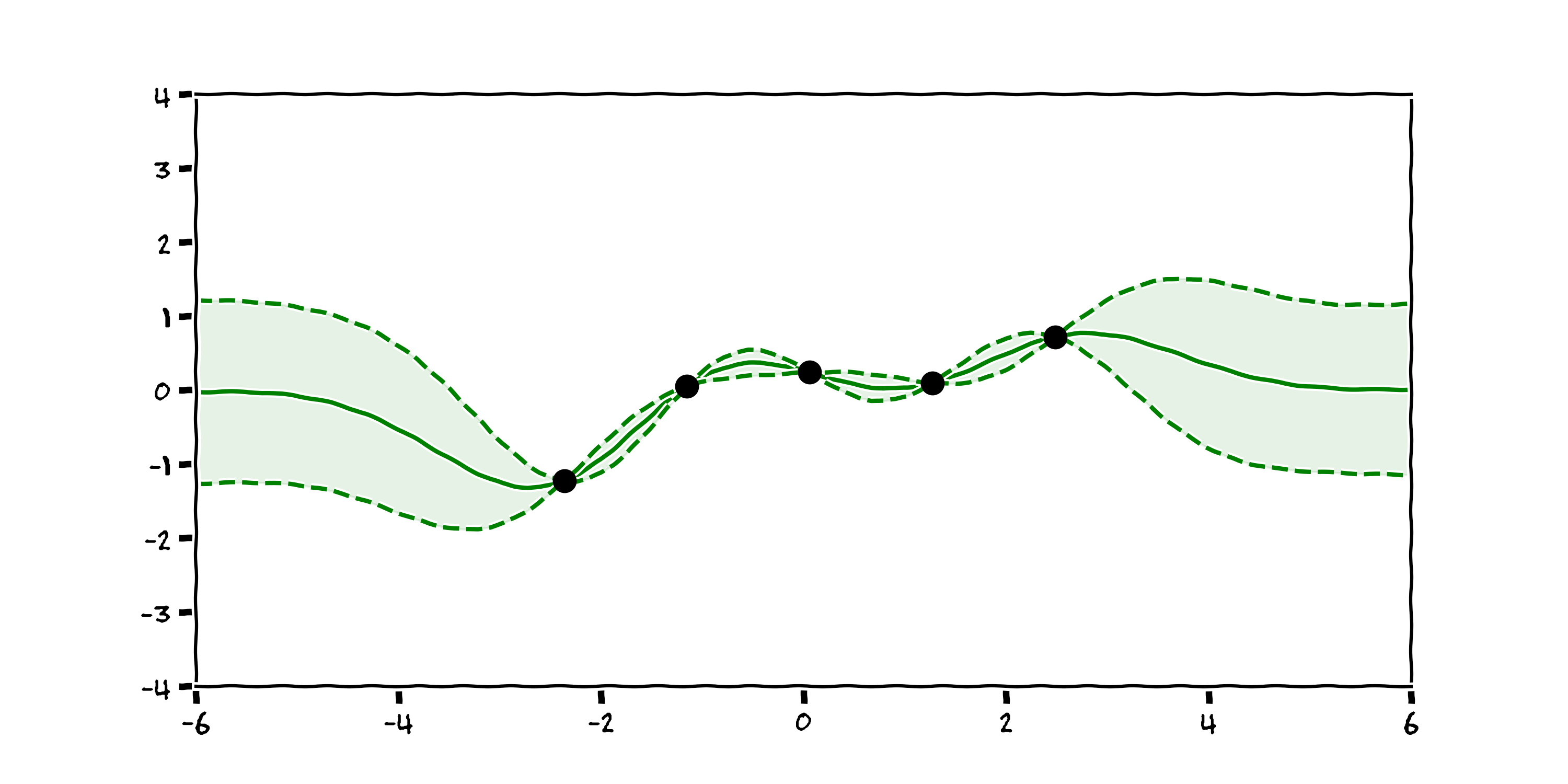
3.3 Drawbacks¶

Expensive to compute; N > ~50,000 prohibitively large
Prior knowledge remains crucial

4. Timeseries Applications¶

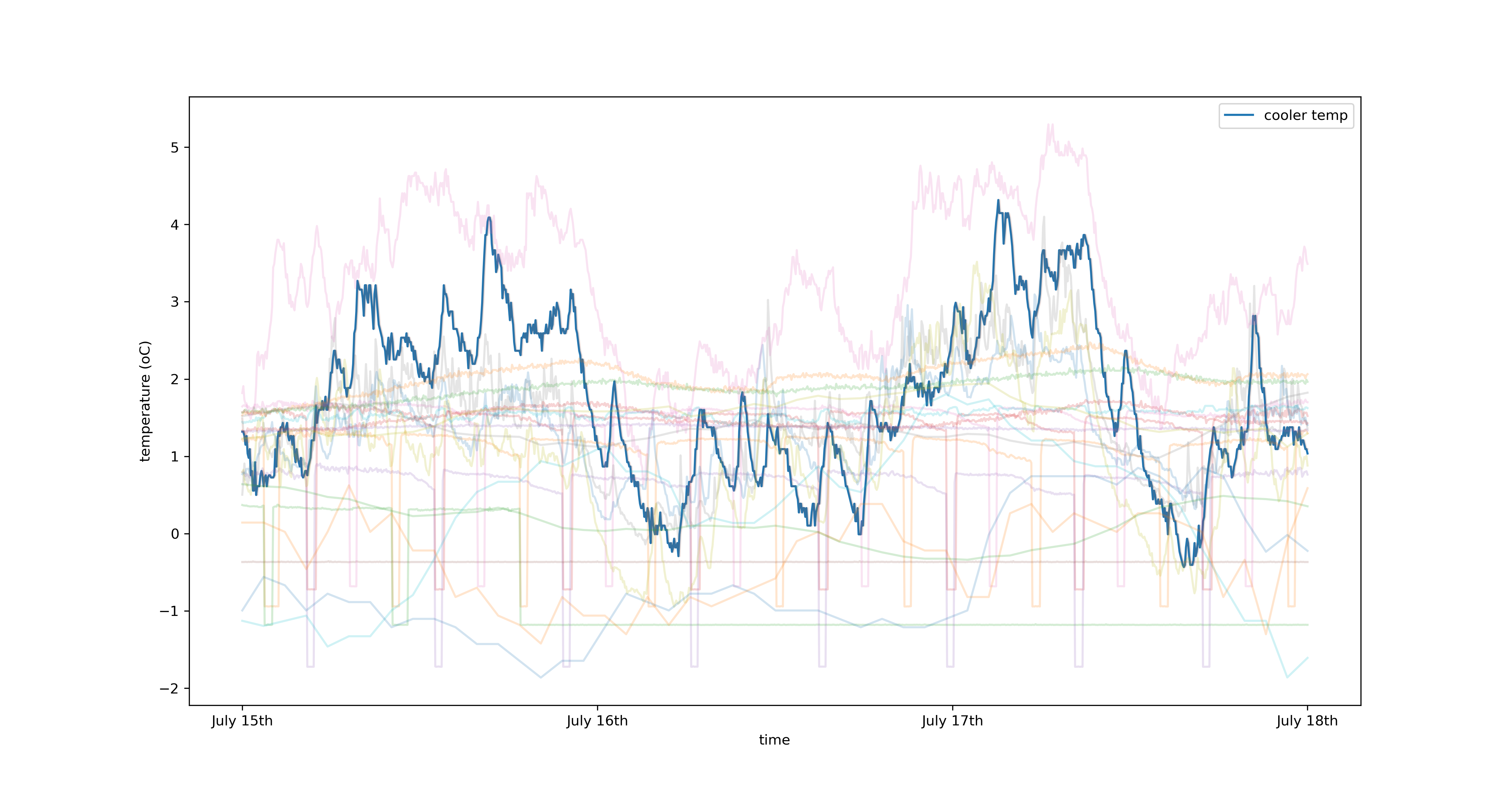
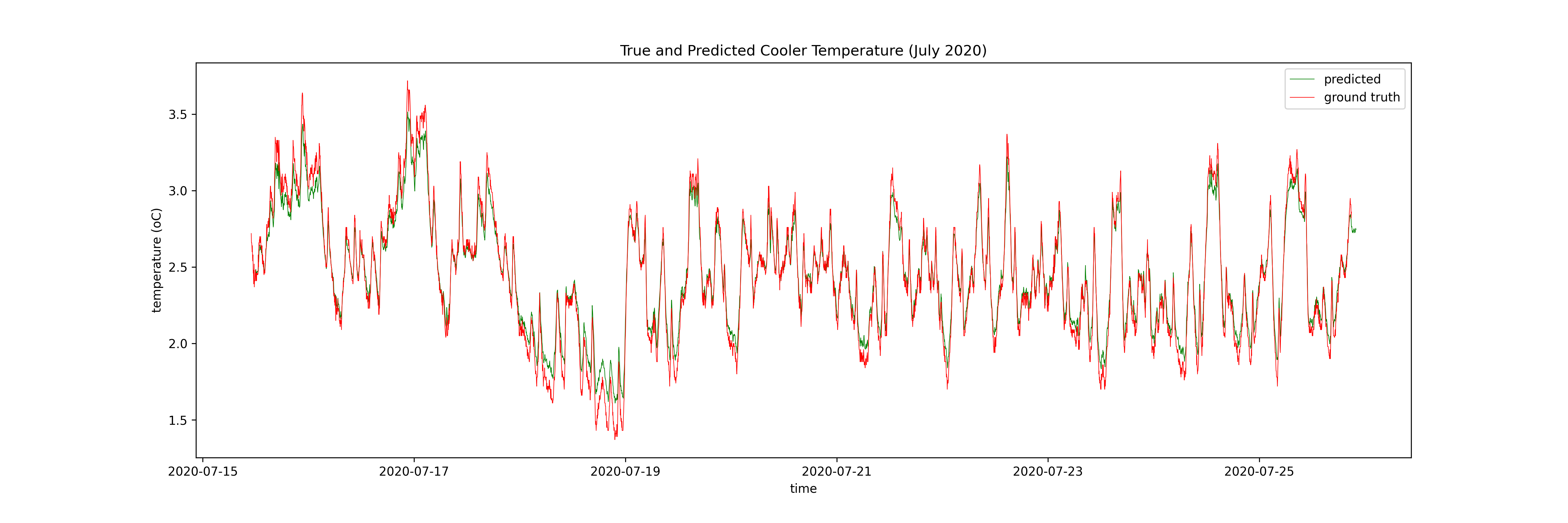
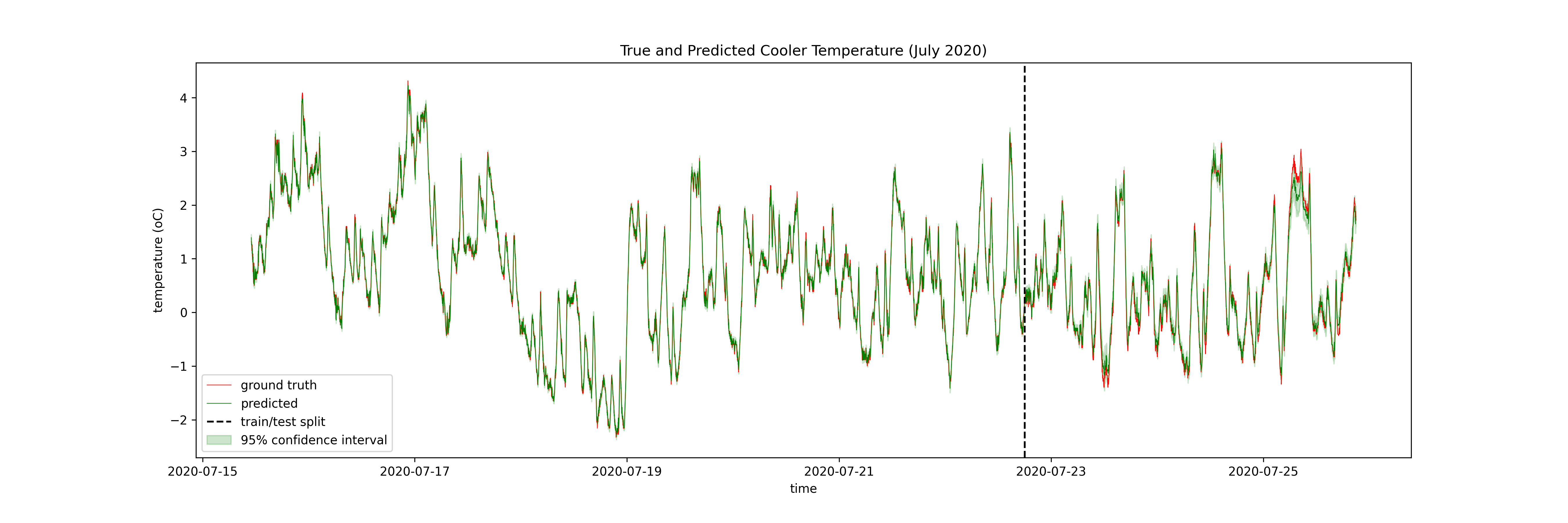
5. Key Takeaways¶

Black box function approximators can model any continuous function in theory
Deterministic techniques effective with large (N > $10^5$) datasets
Probabilistic techniques more robust in low data regimes thanks to uncertainty quantification
GPs are limited by their expensive computations (N must be < $10^5$)
Both approaches can be used to model complex timeseries datasets

Thanks!¶

Notes: https://enjeeneer.io/talks/2021-03-15-xchangeseminar/
Thanks to Carl Henrik Ek, Dept. of Computer Science for inspiring these slides
Questions?