Outline¶
- Motivation: Climate Change Mitigation, Intermittency, and Smart Building Control
- Existing Work
- PEARL: Probabilistic Emission-Abating Reinforcement Learning
- Experimental Setup
- Results and Discussion
- Limitations, Future Work and Conclusions
1. Motivation: Climate Change Mitigation, Intermittency, and Smart Building Control¶

Cullen and Allwood (2010)

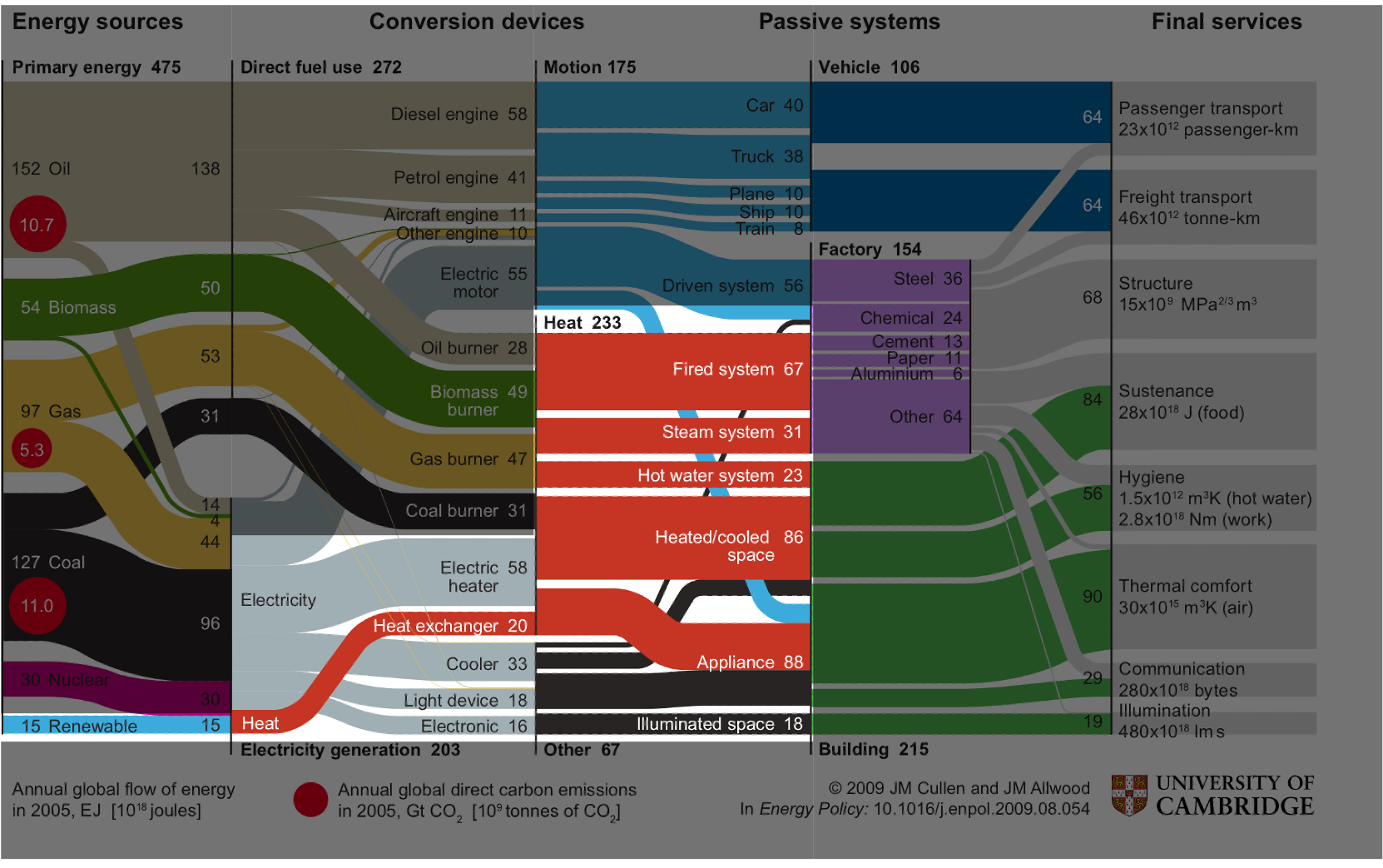
1.2 Intermittency¶

1.2 Intermittency¶
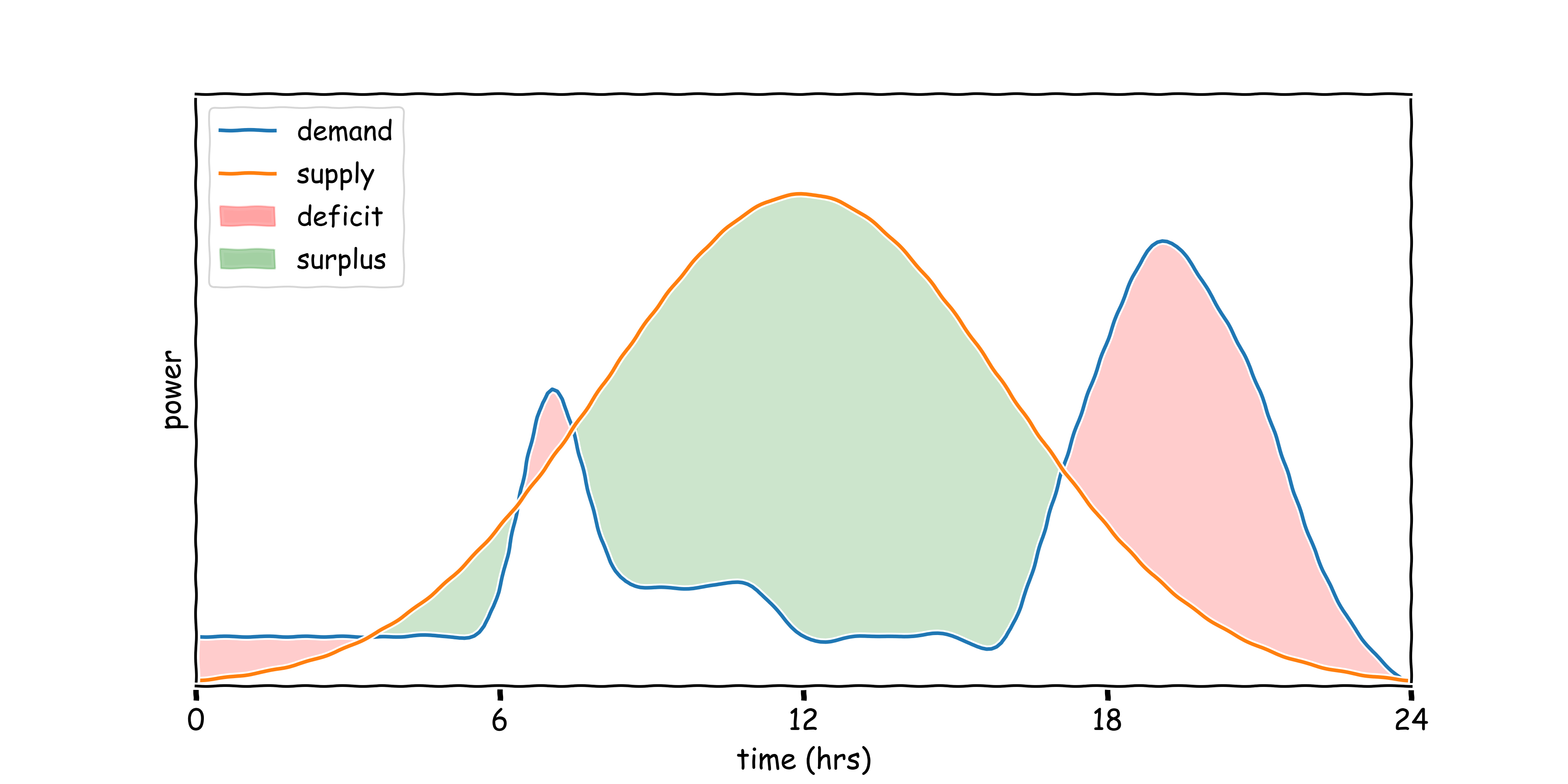
1.3 Smart Building Control¶

2. Existing Work¶
2.1: Model-free RL for Smart Building Control¶

| Authors | Setting | Algorithm | Energy Efficiency | Data Efficiency | In-Situ |
|---|---|---|---|---|---|
| Wei et al. (2017) | 5-zone Building | Deep Q-Learning | ~35% | ~8 years in simulation | ❌ |
| Zhang et al. (2019a) | Office | A3C | ~17% | ~30 years in simulation | ✅ |
| Valladares et al. (2019) | Classroom | Double Q Learning | 5% | ~10 years in simulation | ✅ |
2.2: Model-based RL for Smart Building Control¶

| Authors | Setting | Algorithm | Energy Efficiency | Data Efficiency | In-Situ |
|---|---|---|---|---|---|
| Lazic et al. (2018) | Datacentre | MPC with Linear Model | ~9% | 3 hours live data | ✅ |
2.3: This Work¶
Assumption¶
To scale to every building in the world, we must bypass expensive-to-obtain simulators and perform zero-shot control.
Goal¶
Find new methods that are as data-efficient as Lazic et al. (2018) (i.e ~ 3 hours of live data), yet perform as well as Wei et al. (2017) (i.e. ~ 35% reduction in energy)
3. PEARL: Probabilistic Emission-Abating Reinforcement Learning¶
3.1 End-to-end Agent¶

System ID: Lazic et al. (2018)
Probabilistic Ensembles: Lakshminarayanan et al. (2017)
Trajectory Sampling, CEM and MPC: Botev et al. (2013) and Chua et al. (2018)
3.2 System Identification¶
During a Commissioning Period, $\pi_{systemID}$ is a uniform random walk in control space, bounded to a safe range, with bounded stepwise changes:
$$ a^i[t+1] = \max\left(a_{min}^i, \min(a_{max}^i, a^i[t] + v^i)\right), v^i \sim \text{Uniform}\left(- \Delta ^i, \Delta^i\right) \; \; \; \; \; (1) $$where:
$a^i[t]$ is the value of action $i$ at timestep $t$, with $i \in \mathcal{A}$;
[$a_{min}^i$, $a_{max}^i$] is the safe operating range for action $i$; and
$\Delta^i$ is the maximum allowable change in action $a^i$ between timesteps.
3.3 Learned Dynamics¶
Approximate one-step dynamics: $\tilde{f_{\theta}}: (s_t, a_t) \rightarrow s_{t+1}$
Output: $\tilde{f_\theta}(s_t, a_t) = \mathcal{N}(\mu_\theta(s_t, a_t), \Sigma_\theta(s_t, a_t))$
Randomised Ensemble: $\tilde{f}_\theta(s_t, a_t) = \frac{1}{K} \sum_{k=1}^K \tilde{f}_{\theta_k} (s_t, a_t)$, where $K=5$
Maximum Likelihood Estimation: $Loss(\theta) = \sum_{n=1}^N -\text{log}(P(s_n; \mu_\theta, \Sigma_\theta))$, where $N$=batch size
3.4 Trajectory Sampling, CEM and MPC¶
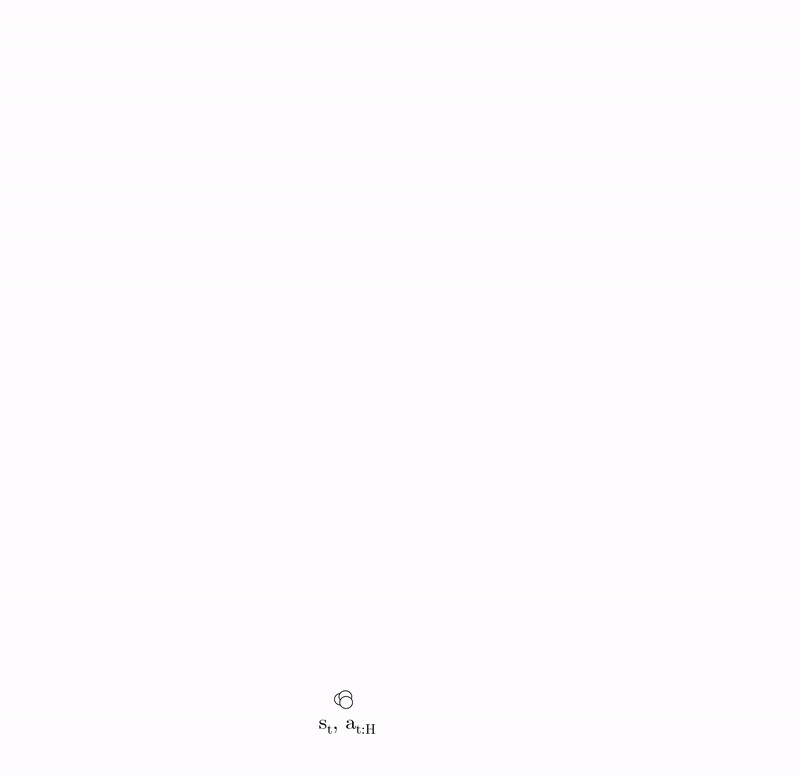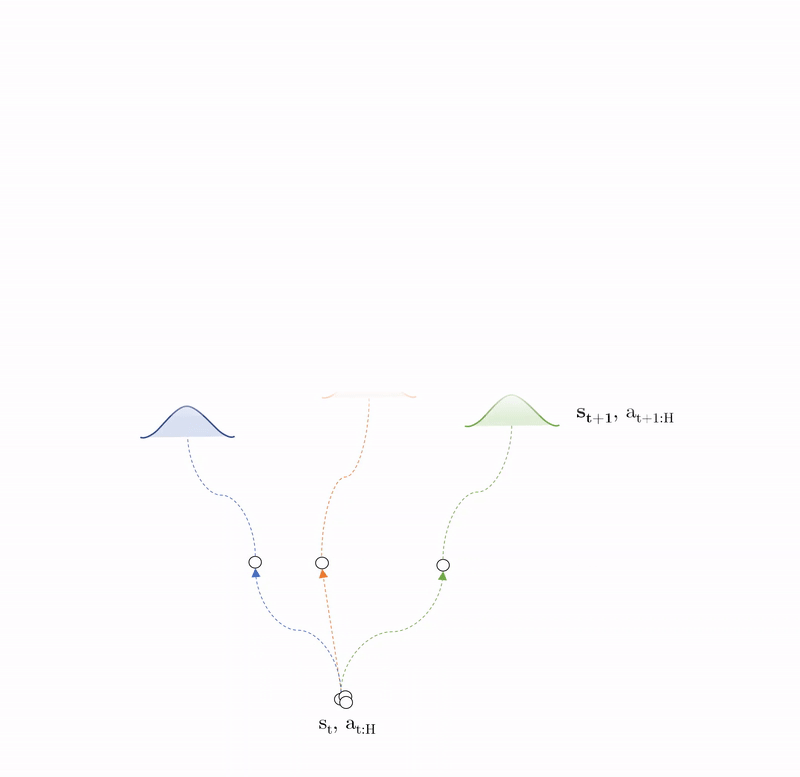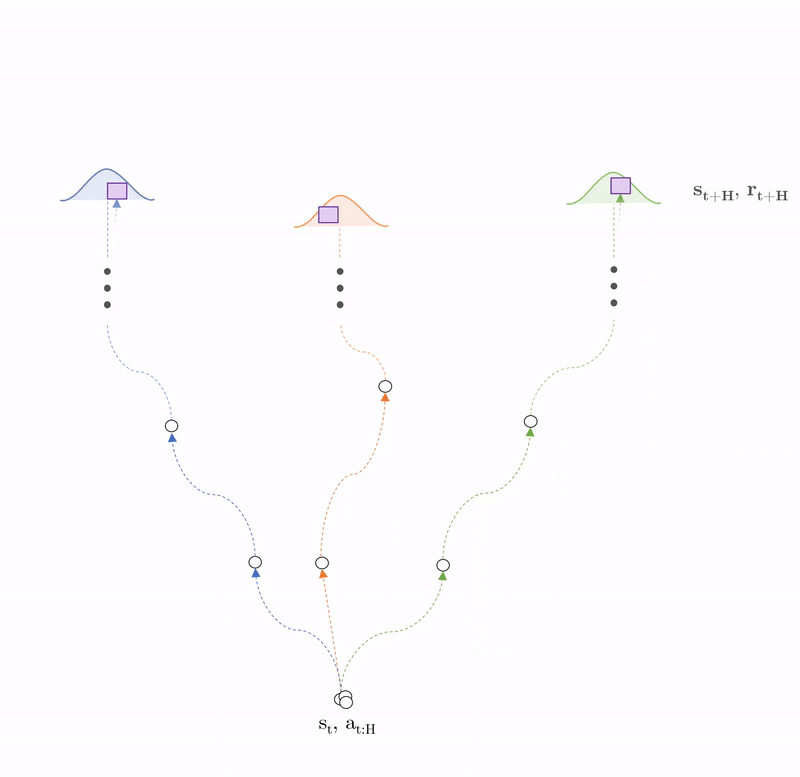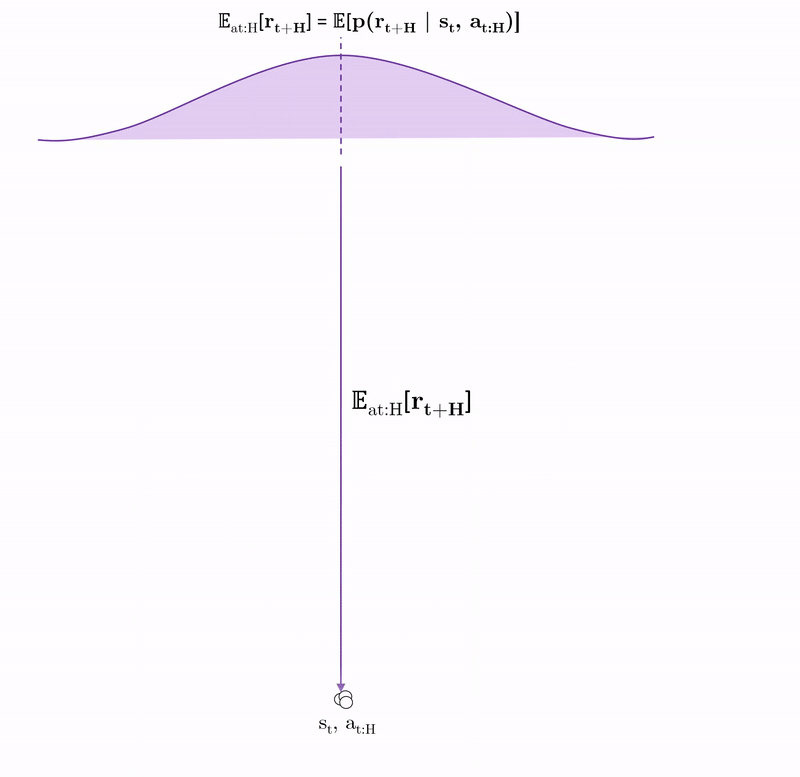
Stochastic policy: $\pi_{CEM}: \mathcal{N}_{\pi}(\mu_{t:t+H}, \sigma_{t:t+H})$
Sample action sequences: $a_{t:t+H}^u \sim \pi_{CEM} \; \forall \; u \in U$
Plan: $s_{t+H}^p = \tilde{f}_\theta(s_t^p, a_{t: t+H}^u) \; \forall \; p \in P$
Optimise: $\text{argmax}_{\boldsymbol{a_{t:t+H}}} \sum_{i=t}^{t+H} \mathbb{E}_{\tilde{f}_\theta}[r(s_i, a_i)]$
where:
$H$ = MPC horizon length (20)
$U$ = no. of candidate action sequences (25)
CEM Iterations = 5
$P$ = no. of trajectory sampling particles (20)
$r(s_i, a_i)$ = reward
3.5 Pseudocode¶

4. Experimental Setup¶
4.1 Environments¶
Experiments conducted in Energym, an open-source building simulation platform built atop EnergyPlus. We run tests in three buildings:
| Mixed-Use | Offices | Seminar Centre | |
|---|---|---|---|
| Location | Athens, Greece | Athens, Greece | Billund, Denmark |
| Floor Area (m$^2$) | 566.38 | 643.73 | 1278.94 |
| Action-space dim | $\mathbb{R}^{12}$ | $\mathbb{R}^{14}$ | $\mathbb{R}^{18}$ |
| State-space dim | $\mathbb{R}^{37}$ | $\mathbb{R}^{56}$ | $\mathbb{R}^{59}$ |
| Thermal Zones | 13 | 25 | 27 |
| Sampling Period | 15 minutes | 15 minutes | 10 minutes |
| Controllable Equipment | Thermostats & AHU Flowrates | Thermostats | Thermostats |
- Standard MDP setup with state-space $\mathcal{S} \in \mathbb{R}^{d_s}$, action-space $\mathcal{A} \in \mathbb{R}^{d_a}$, reward function $r(s_t, a_t)$, and transition dynamics $p(s_{t+1}|s_t, a_t)$.
- Agent attempts to maximise return $G_t = \sum_H \gamma^H r(s_{t+H}, a_{t+H})$, where $\gamma \in [0,1]$ is a discount parameter, and $H$ is a finite time horizon.
4.2 Baselines¶
We compare the performance of our agent against several strong RL baselines, and an RBC:
- Soft Actor Critic (SAC; (Haarnoja et al., 2018))
- Proximal Policy Optimisation (PPO; (Schulman et al., 2017))
- MPC with Deterministic Neural Networks (MPC-DNN; Nagabandi et al. (2018))
- RBC: a generic controller that modulates temperature setpoints following the simple heuristics
- Oracle (Pre-trained SAC): an SAC agent with hyperparameters optimised for each environment and trained for 10 years prior to test time.
4.3 Reward Function¶
Linear combination of an emissions term and a temperature term:
$$ r[t] = r_E[t] + r_T[t] $$with:
$$r_{E}[t] = - \phi \left(E[t] C[t] \right)$$\begin{equation} \label{eq: temperature reward} r_T^i[t]= \begin{cases} 0:& T_{low} \leq T_{obs}^i \leq T_{high} \\ -\theta \min [(T_{low} - T_{obs}^i[t])^2, \; (T_{high} - T_{obs}^i)^2]: & \text{otherwise} \\ \end{cases} \end{equation}where:
- $E[t], C[t],$ and $T_{obs}^i[t]$ are energy-use, grid-carbon intensity and observed temp. at time $t$.
- $\theta$ and $\phi$ are tunable hyperparameters to set relative emphasis of emission minimisation over temp.
- $\theta$ >> $\phi$
- $T_{high}$ and $T_{low}$ are upper and lower bounds on thermal comfort.
The task is to maximise reward (specifically over time horizon $H$) for one year without prior knowledge, historical data or access to the simulator a priori.
5. Results and Discussion¶
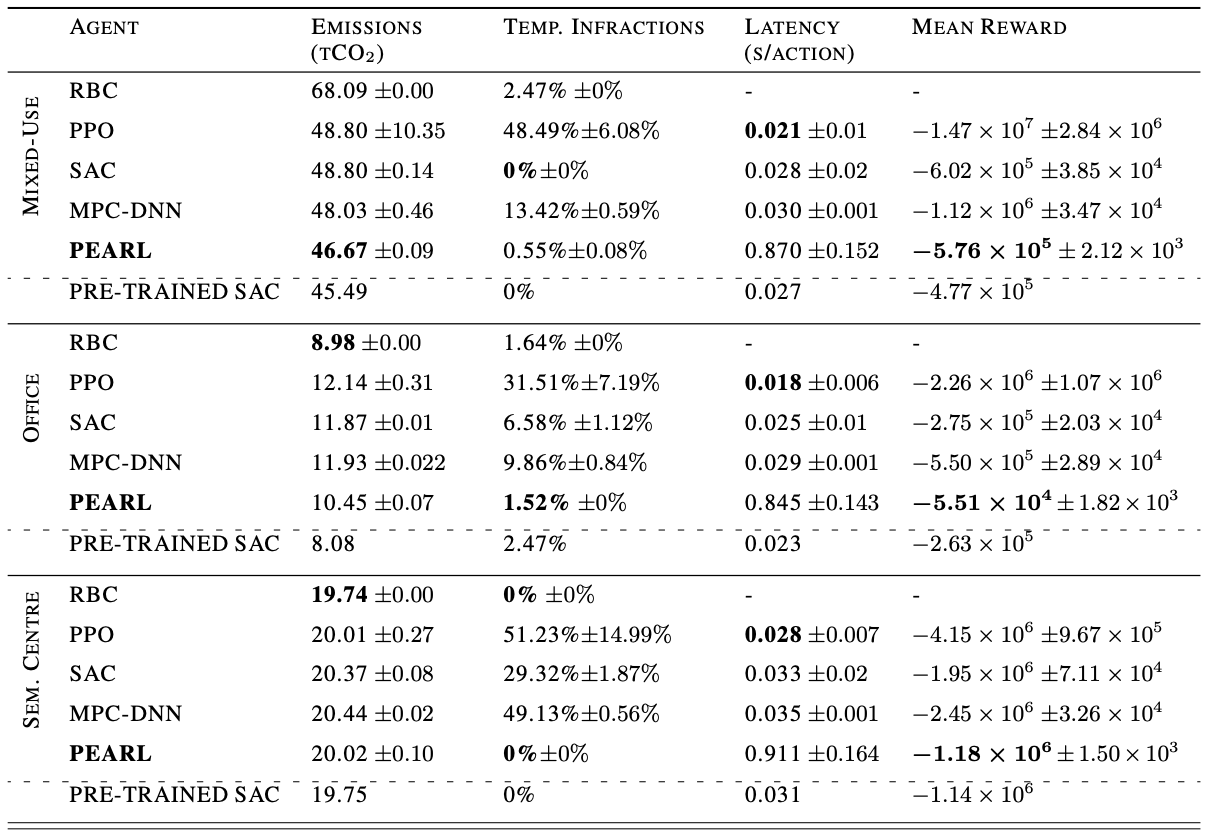
5.1 Performance¶

5.1 Performance¶
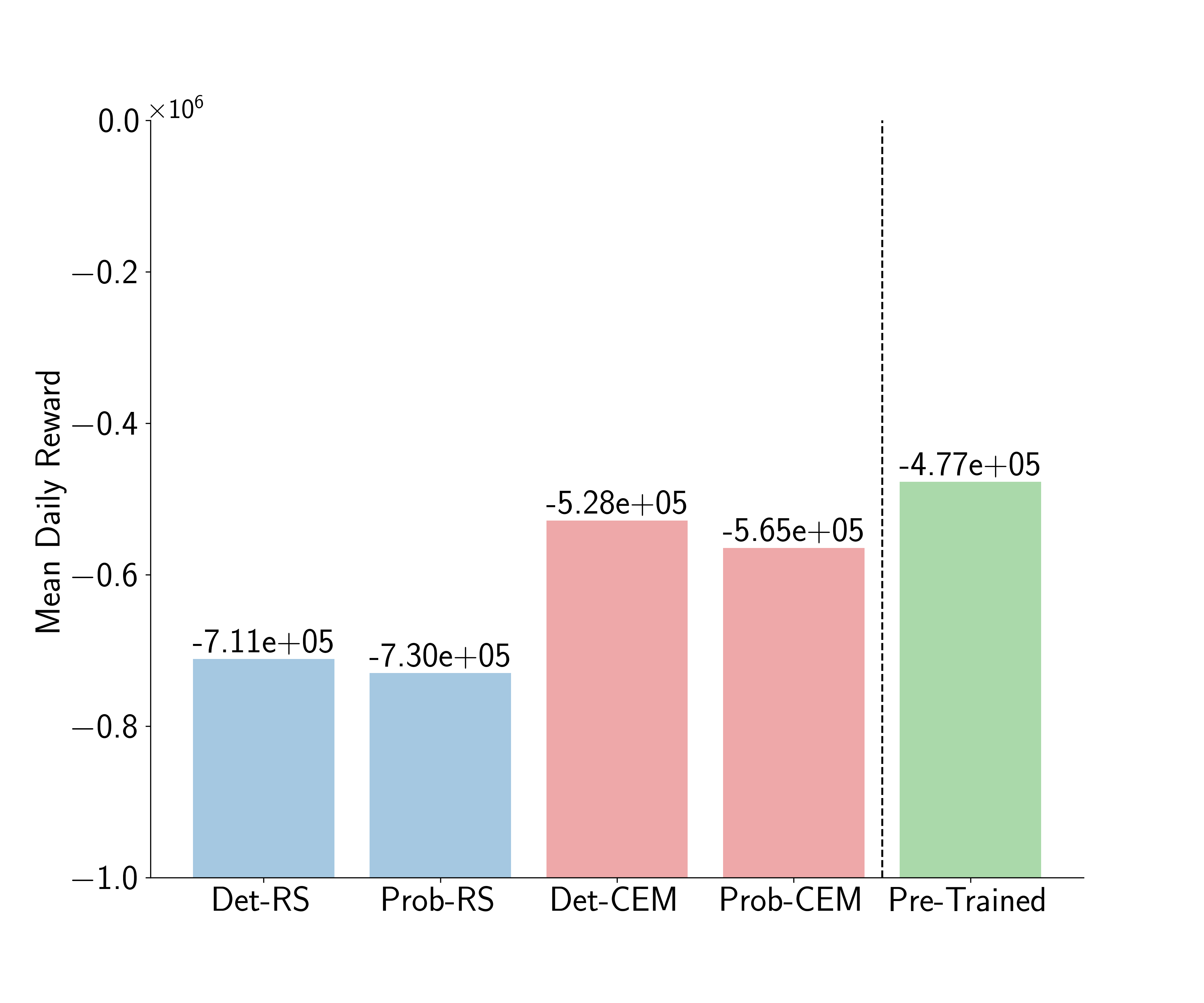
5.3 Agent Decomposition¶
6. Limitations, Future Work and Conclusions¶
6.1 Limitations¶
- Sensor coverage:
- Energym simulations provide large state-spaces; unclear how performance would be affected by lower sensor coverage.
- We assume temporally consistent sensor readings, sensor dropout is likely in the real-world which violates MDP.
- Action-space complexity:
- How complex is too complex?
- How often can we control AHU flowrate in the real world?
- Environments:
- Cannot draw concrete conclusions from tests in three environments for 1 year.
6.2 Future Work¶
- Test in-situ.
- Non-stationarity: how do we deal with it rigorously?
- Scale-up simulations: can we generate two/three orders of magnitude more building sims? We could draw EnergyPlus input files from some representative distribution of building types and train one agent across them.
- Sensor dropout: can we mitigate inconsistent readings with Latent ODEs?
6.3 Conclusions¶
- Efficiently controlling heating and cooling systems in buildings is a useful climate change mitigation tool.
- To scale RL control to every building in the world, we must bypass expensive-to-obtain simulators.
- We show that it is possible to control heating and cooling systems safely by combining system ID and model-based RL.
- Efficiency delta appears to correlate with action-space complexity.
- Choice of action-selection optimizer appears key to safe control.
7. References¶
Chua, K., Calandra, R., McAllister, R., and Levine, S. Deep reinforcement learning in a handful of trials us- ing probabilistic dynamics models. arXiv preprint arXiv:1805.12114, 2018.
Cullen, J. and Allwood, J. The efficient use of energy: Tracing the global flow of energy from fuel to service. Energy Policy, 38(1):75–81, 2010
Ding, X., Du, W., and Cerpa, A. E. Mb2c: Model-based deep reinforcement learning for multi-zone building con- trol. In Proceedings of the 7th ACM International Con- ference on Systems for Energy-Efficient Buildings, Cities, and Transportation, pp. 50–59, 2020.
Haarnoja, T., Zhou, A., Abbeel, P., and Levine, S. Soft actor- critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor, 2018. URL https: arxiv.org/abs/1801.01290.
Lakshminarayanan, B., Pritzel, A., and Blundell, C. Simple and scalable predictive uncertainty estimation using deep ensembles. Advances in neural information processing systems, 30, 2017.
Lazic, N., Lu, T., Boutilier, C., Ryu, M., Wong, E.J., Roy, B., Imwalle, G.: Data center cooling usingmodel-predictive control. In: Proceedings of the Thirty-second Conference on Neural InformationProcessing Systems (NeurIPS-18). pp. 3818–3827. Montreal, QC (2018)
Nagabandi, A., Kahn, G., Fearing, R. S., and Levine, S. Neural network dynamics for model-based deep reinforce- ment learning with model-free fine-tuning. In 2018 IEEE International Conference on Robotics and Automation (ICRA), pp. 7559–7566. IEEE, 2018
Scharnhorst, P., Schubnel, B., Fern ́andez Bandera, C., Sa- lom, J., Taddeo, P., Boegli, M., Gorecki, T., Stauffer, Y., Peppas, A., and Politi, C. Energym: A building model library for controller benchmarking. Applied Sciences, 11 (8):3518, 2021
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and Klimov, O. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347, 2017.
Valladares, W., Galindo, M., Guti ́errez, J., Wu, W.-C., Liao, K.-K., Liao, J.-C., Lu, K.-C., and Wang, C.-C. Energy optimization associated with thermal comfort and indoor air control via a deep reinforcement learning algorithm. Building and Environment, 155:105 – 117, 2019. ISSN 0360-1323
Wei, T., Wang, Y., Zhu, Q.: Deep reinforcement learning for building hvac control. In: Proceedings of the 54th Annual Design Automation Conference 2017. DAC ’17, Association for ComputingMachinery, New York, NY, USA (2017).
Zhang, C., Kuppannagari, S. R., Kannan, R., and Prasanna, V. K. Building hvac scheduling using reinforcement learning via neural network based model approximation. In Proceedings of the 6th ACM international conference on systems for energy-efficient buildings, cities, and trans- portation, pp. 287–296, 2019a.
Zhang, Z., Chong, A., Pan, Y., Zhang, C., and Lam, K. P. Whole building energy model for hvac optimal control: A practical framework based on deep reinforcement learn- ing. Energy and Buildings, 199:472–490, 2019b.
Thanks!¶
Website: https://enjeeneer.io
Slides: https://enjeeneer.io/talks/2022-06-23oxcav/
Twitter: @enjeeneer
Questions?

